5 Zusammenhangsmaße

Zusammenhänge sind das Herz (fast) aller statistischer Analysen. Im Folgenden lernen wir die Berechnung einer Reihe von Kennzahlen kennen, welche den Zusammenhang zwischen zwei Variablen ausdrücken. Diese variieren je nachdem ob sie nur die Stäke oder auch die Richtung eines Zusammenhangs ausdrücken. Der Abstand zur Null dient dabei als Indikator für die Stärke des Zusammenhangs - je größer der Abstand zur Null, desto stärker der Zusammenhang:

Wert der Kennzahl (\(K\))	Grad des Zusammenhangs
\(K\) = 0	Keiner
0,00 ≤ \(K\) < 0,05	Praktisch keiner
0,05 ≤ \(K\) < 0,25	Geringer
0,25 ≤ \(K\) < 0,50	Mittlerer
0,50 ≤ \(K\) < 1,00	Starker
\(K\) = 1,00	Perfekter

Zusammenhangsmaße für metrische und ordinale Variablen geben mittels der Vorzeichen auch die Zusammenhangsrichtung an, sie variieren zwischen -1 und +1.

5.1 Metrisch skalierte Variablen

Wir sehen uns den (möglichen) Zusammenhang zwischen dem Alter (age) und dem BMI (hs18) der Befragten an. Dazu schließen wir zunächst die Missings aus und wählen die Befragten aus dem Jahr 2012 aus:

cd ""
use  Allbus_1980-2018.dta   
keep if year == 2012
mvdecode age hs18, mv(-32 -13)

(64681 observations deleted)

         age: 7 missing values generated
        hs18: 1859 missing values generated

5.1.1 Korrelationskoeffizient

Zur Bestimmung eines Zusammenhangs zwischen zwei metrischen Variablen empfiehlt sich der Korrelationskoeffizient nach Pearson. Dieser ist definiert als die Kovarianz dividiert durch die jeweiligen Standardabweichungen der beiden Variablen und liegt im Intervall [-1,1]. Die Standardabweichung hatten wir in Session 4 kennengelernt, die Kovarianz erfasst die Lage der Datenpunkte relativ zu den Mittelwerten der beiden interessierenden Variablen (liegen Punkte > \(\bar{x}\) auch \(>\bar{y}\)?):

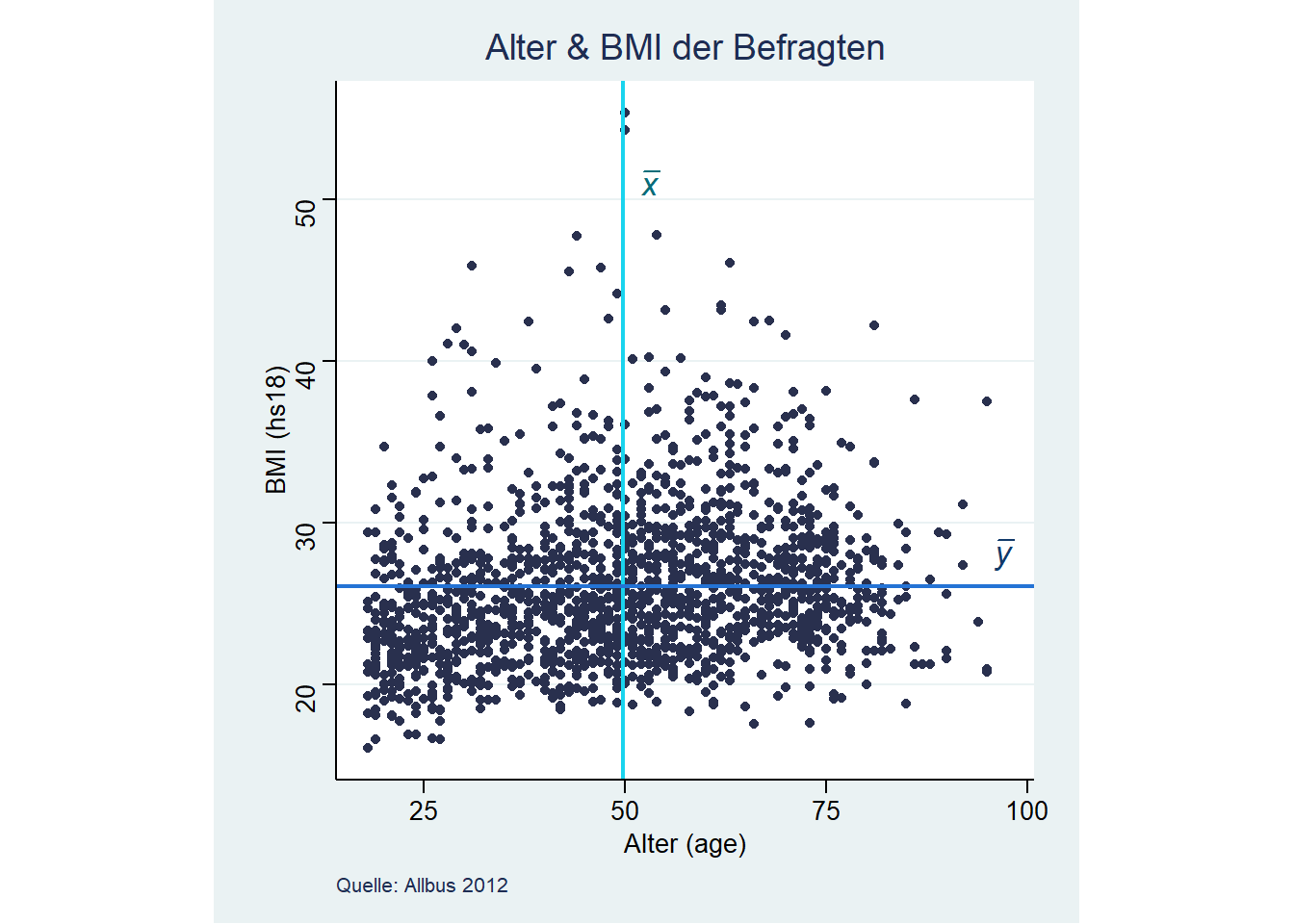In Stata können wir den Korrelationskoeffizienten mit corr berechnen:

corr age hs18

(obs=1620)

             |      age     hs18
-------------+------------------
         age |   1.0000
        hs18 |   0.2127   1.0000

Es handelt sich also um einen geringen Zusammenhang.

5.1.2 Regression

Regressionsmodelle zeigen uns den (linearen) Trend zwischen zwei Variablen. Hier geht es darum, um wie sich im Durchschnitt var2 verändert, wenn sich var1 um eine Einheit erhöht. var2 ist also unsere abhängige, var1 unsere unabhängige Variable - wir möchten var2 mit var1 vorhersagen. Im Folgenden sehen wir, dass Regressionsmodelle mit reg erstellt werden können und wie wir den Output interpretieren können. Falls Sie nochmal mehr zu den Grundlagen erfahren wollten, findet sich hier eine ausführlichere Erklärung.

Wir betrachten einen kleinen Beispieldatensatz mit lediglich 4 Fällen und zwei metrischen Variablen var1 und var2:

use "https://github.com/filius23/Stata_Skript/raw/master/regression_bsp.dta", clear

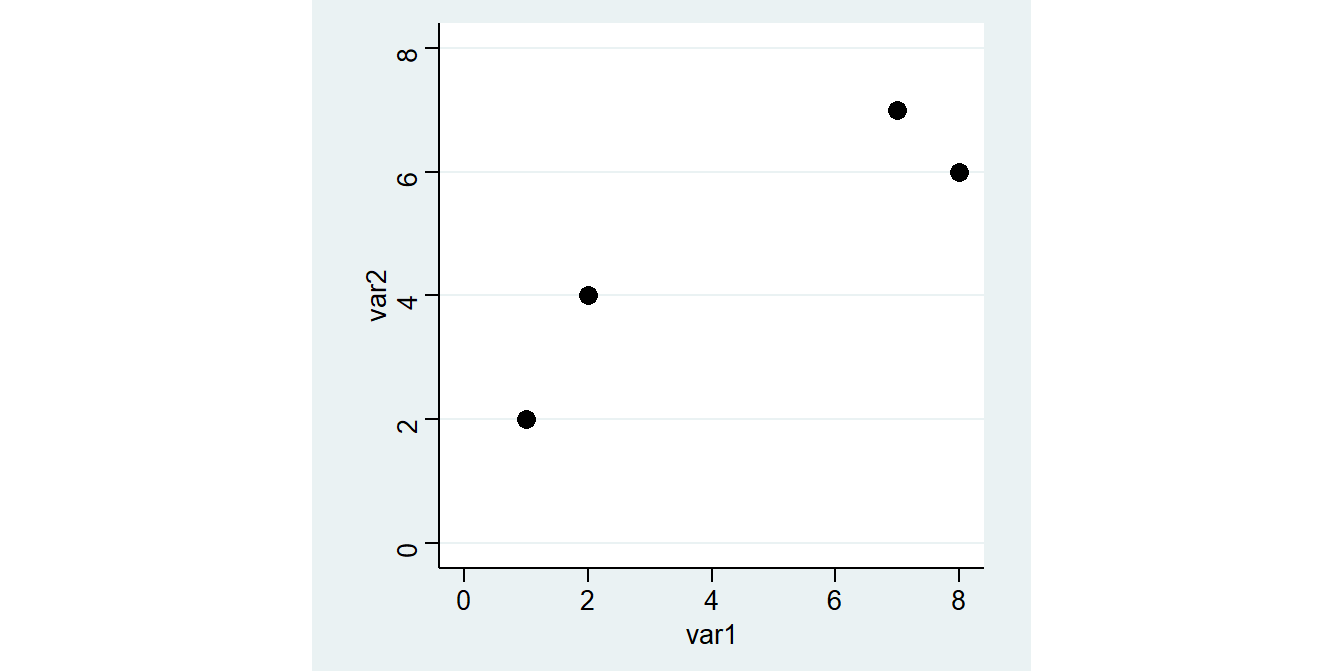
Mit Regressionsmodellen können wir lineare Zusammenhänge zwischen zwei metrischen Merkmalen untersuchen. In Stata können wir eine Regression mit dem reg Befehl berechnen:

reg var2 var1

      Source |       SS       df       MS              Number of obs =       4
-------------+------------------------------           F(  1,     2) =   11.07
       Model |  12.4932432     1  12.4932432           Prob > F      =  0.0797
    Residual |  2.25675676     2  1.12837838           R-squared     =  0.8470
-------------+------------------------------           Adj R-squared =  0.7705
       Total |       14.75     3  4.91666667           Root MSE      =  1.0623

------------------------------------------------------------------------------
        var2 |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        var1 |   .5810811   .1746331     3.33   0.080    -.1703044    1.332467
       _cons |   2.135135   .9485004     2.25   0.153    -1.945933    6.216203
------------------------------------------------------------------------------

Hier steht jetzt eine ganze Menge an Informationen, die wir uns im Folgenden genauer ansehen werden.

---

Ein positiver Wert unter Coef. in der Zeile von var1 bedeutet, dass unsere Gerade von links nach rechts ansteigt und ein negativer eine fallende Linie bedeuten würde. Der Wert unter var1 gibt an, um wieviel sich die Gerade pro “Schritt nach rechts” nach oben/unten verändert.

Die Gerade steigt also pro Einheit von var1 um 0.5810811.

Der Wert neben _cons gibt uns Auskunft darüber, wie hoch der vorhergesagte Wert für var2 wäre, wenn var1 = 0.

Für var1 = 0 würden wir var2 = 2.135135 vorhersagen.

Außerdem erkennen wir unter R-squared die Modellgüte unseres Regressionsmodells. \(R^2\) gibt die prozentuale Verbesserung der Vorhersgen durch die Gerade aus reg im Vergleich zum arithmetische Mittel an. \(R^{2}\) bezieht sich auf die Verringerung der Residuen durch das reg-Modell im Vergleich zur Mittelwertregel.

Unser Regressionsmodell kann also 84,7% der Streuung um den Mittelwert erklären.

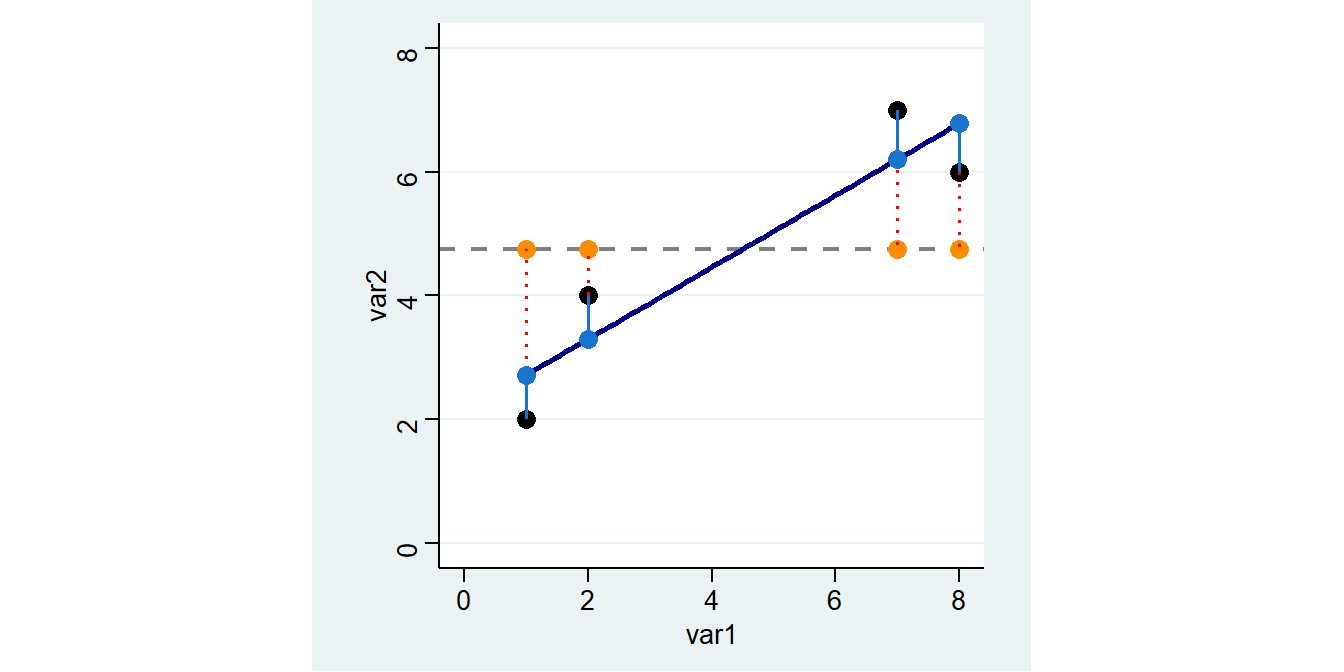
Außerdem sehen wir oben links in der Spalte SS die “Sum of Squares”: unter Total ist die Summe der quadrierten Abweichungen der beobachteten Werte vom arith. Mittel angegeben (die Abstände zwischen den orangen und schwarzen Punkten: 14.75). Residual gibt die Summe der Abweichungsquadrate zwischen den beobachteten Werten und den vorhergesagten Werten der Regression (die Abstände zwischen den schwarzen und den blauen Punkten:2.256..).

---

5.1.3 vorhergesagte Werte

Die vorhergesagten Werte aus reg var2 var1 entsprechen einfach der Summe aus dem Wert neben _cons und dem Koeffizienten neben var1 multipliziert mit dem jeweiligen Wert für var1. Wir starten also sozusagen bei var2=0 und gehen dann eben x Schritte entlang der Geraden.

reg var2 var1, noheader /// noheader macht den Output übersichtlicher

        var2 |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        var1 |   .5810811   .1746331     3.33   0.080    -.1703044    1.332467
       _cons |   2.135135   .9485004     2.25   0.153    -1.945933    6.216203
------------------------------------------------------------------------------

Vorhergesagte Werte für var2 werden mit \(\widehat{var2}\) bezeichnet - das \(\widehat{}\) steht dabei für “geschätzt”:

\[\widehat{var2}=\texttt{Intercept} + 0.5811 \times \texttt{var1}\]
Für die erste Zeile ergibt sich also folgender vorhergesagter Wert: 2.1351+0.5811*1= 2.7162

Wir könnten also auch einen vorhergesagten Wert für einen beliebigen Wert von var1 berechnen, für 5:

display 2.1351+0.5811*5

5.0406

Alternativ können wir uns die Tipparbeit auch sparen, indem wir erst reg laufen lassen und dann mit _b auf die Ergebnisse zugreifen:

reg var2 var1
display _b[_cons] + _b[var1] * 5

5.0405405

Mit predict können wir jeweils die vorhergesagten Werte für die Ausprägungen von var1 im Datensatz berechnen und in einer neuen Variable pred_vorher ablegen:

predict pred_vorher, xb

Hier wird also gerechnet:

\[2.1351 + 0.5810811 * 1 = 2.716216\] \[2.1351 + 0.5810811 * 2 = 3.297297\] \[2.1351 + 0.5810811 * 7 = 6.202703\] \[2.1351 + 0.5810811 * 8 = 6.783784\]

  var1 var2 pred_vorher mean_var2
1    1    2    2.716216      4.75
2    2    4    3.297297      4.75
3    7    7    6.202703      4.75
4    8    6    6.783784      4.75

Die Grafik oben zeigt wie Vorhersagen auf Basis des Regressionsmodells aussehen: Sie entsprechen den Werten auf der blauen Geraden (der sog. Regressionsgeraden) an den jeweiligen Stellen für var1.

5.1.4 Korrelation und Regression

---

Übung1

---

5.2 Ordinal skalierte Variablen

Ein klassisches ordinales Merkmal ist die Bildung (educ):

educ	Schulabschluss
1	Schule beendet ohne Abschluss
2	Volks-/Hauptschulabschluss bzw. Polytechnische Oberschule (8. oder 9. Klasse)
3	Mittlere Reife, Realschulabschluss bzw. Polytechnische Oberschule (10. Klasse)
4	Fachhochschulreife (Abschluss einer Fachoberschule etc.)
5	Abitur bzw. Erweiterte Oberschule mit Abschluss 12. Klasse (Hochschulreife)
6	Anderer Schulabschluss, und zwar: ______
7	Noch Schüler

Wir sehen uns den Zusammenhang der Bildung der Befragten mit der Einstellung zum Zuzug von Asylsuchenden (mi02) an:

Wir sehen uns den (möglichen) Zusammenhang zwischen diesen beiden Merkmalen an. Dazu definieren die negativen Ausprägungen sowie die Kategorien (7) “noch Schüler” und (6) “anderer Schulabschluss” als Missing, um eine klare ordinale Rangfolge für educ zu erhalten (je höher,desto höher der Bildungsabschluss). Wir sehen uns den Zusammenhang für das Jahr 1990 an:

cd ""
use  "Allbus_1980-2018.dta",clear
keep if year == 1990
mvdecode educ, mv(-9 6 7)
mvdecode mi02, mv(-9 -8 -7)

        educ: 65 missing values generated

        mi02: 97 missing values generated

So sieht die Verteilung zunächst in einer Kreuztabelle aus:

tab educ mi02

       ALLGEMEINER |     ZUZUG VON: ASYLSUCHENDEN
    SCHULABSCHLUSS | UNEINGESC  ZUZUG BEG  GANZ UNTE |     Total
-------------------+---------------------------------+----------
    OHNE ABSCHLUSS |         7         18         36 |        61 
VOLKS-,HAUPTSCHULE |       123        659        600 |     1,382 
    MITTLERE REIFE |       137        390        177 |       704 
FACHHOCHSCHULREIFE |        48        101         21 |       170 
    HOCHSCHULREIFE |       232        287         53 |       572 
-------------------+---------------------------------+----------
             Total |       547      1,455        887 |     2,889 

Auch hier fragen wir uns jetzt: sind die Werte von mi02 tendenziell höher oder niedriger bei höheren Werten von educ? Allerdings ist hier der Korrelationskoeffizient nicht adäquat, die hier die Abstände zwischen den Kategorien nicht gleichmäßig sind (es handelt sich ja um ordinale Merkmale). Daher müssen hier spezifische Zusammenhangsmaße für ordinale Variablen verwendet werden.

5.2.1 Spearman- Rangkorrelation

Zur Bestimmung eines Zusammenhangs zwischen zwei ordinal skalierten Variablen empfiehlt sich der Spearman-Rangkorrelationskoeffizient (\(\rho\)). Für den Rangkorrelationskoeffizienten werden die Werte der Variablen in Ränge überführt und dann mit diesen Rängen den Korrelationskoeffizient berechnet. Wir können den Rangkorrelationskoeffizienten mit spearman berechnen:

spearman educ mi02

 Number of obs =    2889
Spearman's rho =      -0.3749

Test of Ho: educ and mi02 are independent
    Prob > |t| =       0.0000

Es zeigt sich also mit einem Korrelationskoeffizienten von 0.37 ein mittel-starker, negativer Zusammenhang. Das negative Vorzeichen des Zusammenhangs deutet darauf hin, dass mit einer höheren Ausprägung von educ tendenziell niedrigere Werte für mi02 einher gehen: eine höhere Schulbildung geht mit einer positiveren Haltung gegenüber dem Zuzug von Asylsuchenden einher.

5.2.2 Konkordanzmaße

tab educ mi02

       ALLGEMEINER |     ZUZUG VON: ASYLSUCHENDEN
    SCHULABSCHLUSS | UNEINGESC  ZUZUG BEG  GANZ UNTE |     Total
-------------------+---------------------------------+----------
    OHNE ABSCHLUSS |         7         18         36 |        61 
VOLKS-,HAUPTSCHULE |       123        659        600 |     1,382 
    MITTLERE REIFE |       137        390        177 |       704 
FACHHOCHSCHULREIFE |        48        101         21 |       170 
    HOCHSCHULREIFE |       232        287         53 |       572 
-------------------+---------------------------------+----------
             Total |       547      1,455        887 |     2,889 

Ein weiteres Zusammenhangsmaß für ordinale Variablen sind Konkordanzmaße wie Kendall’s \(\tau\). Hierfür die Werteverhältnisse gezählt:

• \(\tau_a\): Differenz der konkordaten (C) und diskordanten (D) Paarvergleiche als Anteil an allen möglichen Paarvergleichen \(\frac{n\times(n-1)}{2}\):

\[\tau_a=\frac{C-D}{\frac{n\times(n-1)}{2}}\] Nachteil: Bei Bindungen in X u. Y Maximalwerte (-1; +1) nicht zu erreichen

• \(\tau_b\): Differenz der konkordaten (C) und diskordanten (D) Paarvergleiche als Anteil an allen möglichen Paarvergleichen \(\frac{n\times(n-1)}{2}\) unter Ausschluss von Bindungen in X und Y

\[\tau_{b}=\frac{C-D}{\sqrt{(C+D+T_x)\times(C+D+T_y)}}\] Nachteil: Bei Bindungen in X o. Y Maximalwerte (-1; +1) nicht zu erreichen

• Goodman & Kruskal’s \(\gamma\) ignoriert die Bindungen vollständig:

\[\gamma=\frac{C-D}{C+D}\]

Zur Berechnung in Stata können wir ktau verwenden:

ktau educ mi02

  Number of obs =    2889
Kendall's tau-a =      -0.2151
Kendall's tau-b =      -0.3350
Kendall's score = -897325
    SE of score =   44116.299   (corrected for ties)

Test of Ho: educ and mi02 are independent
     Prob > |z| =       0.0000  (continuity corrected)

Auch hier zeigt sich eine Zusammenhangsstärke in der gleichen Größenordnung wie beim Rangkorrelationskoeffizienten (\(\tau_a\) = -0.2151 und \(\tau_b\) = -0.3350). Zudem ist auch hier das Vorzeichen negativ: educ korreliert negativ mit mi02. Der Wert von Kendall’s \(\tau_a\) ist deutlich niedriger als von Kendall’s \(\tau_b\), da hier der Nenner durch die Berücksichtigung aller möglichen Paarvergleiche größer wird, der Zähler aber für beide Varianten von Kendall’s \(\tau\) gleich definiert ist.

Ein weiteres Maß ist Goodman & Kruskal’s \(\gamma\), dieses bekommen wir mit der Option ,gamma in tab:

tab educ mi02, gamma

       ALLGEMEINER |     ZUZUG VON: ASYLSUCHENDEN
    SCHULABSCHLUSS | UNEINGESC  ZUZUG BEG  GANZ UNTE |     Total
-------------------+---------------------------------+----------
    OHNE ABSCHLUSS |         7         18         36 |        61 
VOLKS-,HAUPTSCHULE |       123        659        600 |     1,382 
    MITTLERE REIFE |       137        390        177 |       704 
FACHHOCHSCHULREIFE |        48        101         21 |       170 
    HOCHSCHULREIFE |       232        287         53 |       572 
-------------------+---------------------------------+----------
             Total |       547      1,455        887 |     2,889 

                    gamma =  -0.5065  ASE = 0.021

Auch Goodman & Kruskal’s \(\gamma\) deutet auf einen negativen Zusammenhang hin, hier ist die Stärke mit (-0.5065) aber deutlich höher. Dies ist auf die Berücksichtigung der Bindungen zurückzuführen: hier werden alle Bindungen ausgeschlossen, also auch Paarvergleiche mit Bindungen nur auf einer Variable. Es reduziert sich also der Nenner, somit ergibt sich im Ergebnis ein höherer Koeffizient für Goodman & Kruskal’s \(\gamma\) als für Kendall’s \(\tau_b\).

Insgesamt ist also von einem mittleren Zusammenhang zwischen educ und mi02 auszugehen.

---

Übung2

---

5.3 Nominal skalierte Variablen

cd ""
use  "Allbus_1980-2018.dta",clear
keep if year == 2014 & dh01 > 0 & dh04 > 0 & aq03 > 0

(64715 observations deleted)

Unser Beispiel für nominal skalierte Variablen dreht sich um die Frage: Haben allein lebende Befragte eher ein Haustier als Befragte, die mit weiteren Personen zusammenleben?

Dazu betrachten wir die Variablen aq03 und dh01, später auch noch dh04:

aq03	Haben Sie einen Hund oder eine Katze in Ihrem Haushalt?
	1 Ja, Hund
	2 Ja, Katze
	3 Ja, beides
	4 Nein, keines von beiden
dh01	Wohnen außer ihnen noch weitere Personen in diesem Haushalt?
	1 Ja
	2 Nein, ich lebe allein
dh04	Gesamtzahl der Personen im Haushalt

Ausgangspunkt der Zusammenhangsmaße für nominale Merkmale ist die Kontingenztabelle der beiden Variablen:

tab aq03 dh01

 HUND ODER KATZE | MEHRPERSONENHAUSHALT?
    IM HAUSHALT? | MEHRPERSO  EINPERSON |     Total
-----------------+----------------------+----------
            HUND |       350         41 |       391 
           KATZE |       502         65 |       567 
          BEIDES |       116          9 |       125 
KEINS VON BEIDEN |     1,784        579 |     2,363 
-----------------+----------------------+----------
           Total |     2,752        694 |     3,446 

Um diese Tabelle für den Einstieg noch etwas übersichtlicher zu halten, fassen wir die Hunde- und Katzenbesitzer*innen zusammen. Das geht mit gen: wir formulieren darin eine Bedingung und wenn diese zutrifft wird der erste Wert eingesetzt, wenn nicht wird der zweite Wert eingesetzt. Hier fragen wir also ab, ob aq03 gleich 4 ist - dann wird eine 0 eingesetzt, ansonsten eine 1:

gen aq03b = (aq03 == 4) if !missing(aq03)
list aq03 aq03b in 1/10, nol

   aq03 aq03b
1     4     0
2     2     1
3     3     1
4     4     0
5     4     0
6     4     0
7     2     1
8     4     0
9     4     0
10    1     1

Die daraus resultierende Kontingenztabelle ist schön übersichtlich:

tab aq03b dh01

           | MEHRPERSONENHAUSHALT?
     aq03b | MEHRPERSO  EINPERSON |     Total
-----------+----------------------+----------
         0 |       968        115 |     1,083 
         1 |     1,784        579 |     2,363 
-----------+----------------------+----------
     Total |     2,752        694 |     3,446 

\(\rightarrow\) Wie viele Personen leben also allein und haben kein Haustier?¹

5.3.1 Odds Ratio

Die Odds Ratio geben das Verhältnis der bedingten Häufigkeiten an. Wir berechnen in beiden Spalten (also getrennt nach Haushaltsgröße) jeweils die Odds, dass ein*e Befragte*r ein Haustier besitzt (also aq03b = 1). Odds sind dabei immer das Verhältnis \(\frac{interessierende\;Ausprägung}{alle\;anderen\;Ausprägungen}\). Dann setzen wir die Chancen ins Verhältnis zueinander:

\[\text{Odds Haustier in MP-HH} = \frac{968}{1784} = 0.5426009\] \[\text{Odds Haustier allein} = \frac{115}{579} = 0.1986183\] \[\text{Odds Ratio Haustier MP vs. allein} = \frac{0.5426009}{0.1986183} = 2.731878\] \[\text{Odds Ratio Haustier allein vs. MP HH} = \frac{0.1986183}{0.5426009}=0.3660486\] Interpretation:

• Alleinlebende Befragte haben im Vergleich zu Befragten, die mit anderen Personen zusammen wohnen, die 0.366-fache Chance Haustiere zu haben.
• Befragte, die mit anderen Personen zusammen wohnen, haben im Vergleich zu alleinlebenden Befragten die 2.732-fache Chance Haustiere zu haben.

Odds Ratios sind aber auch aus “größeren” Tabellen berechenbar - zB können wir auch die exakte Haushaltsgröße dh04 sowie die detaillierten Kategorien zum Haustierbesitz (aq03) verwenden:

tab aq03 dh04

 HUND ODER KATZE |                                    ANZAHL DER HAUSHALTSPERSONEN
    IM HAUSHALT? |         1          2          3          4          5          6          7          8         10 |     Total
-----------------+---------------------------------------------------------------------------------------------------+----------
            HUND |        41        153         86         73         32          4          2          0          0 |       391 
           KATZE |        65        250        120         91         31          6          4          0          0 |       567 
          BEIDES |         9         43         29         26         11          5          1          0          1 |       125 
KEINS VON BEIDEN |       579        938        388        342         91         16          7          2          0 |     2,363 
-----------------+---------------------------------------------------------------------------------------------------+----------
           Total |       694      1,384        623        532        165         31         14          2          1 |     3,446 

Jetzt könnten wir den Odds Ratio für Haustierbesitz von allein Lebenden im Vergleich zu Befragten mit einer HH-Größe von 2 berechnen. Dazu setzen wir für die jeweiligen Spalten (weil die HH-Größe dh04 in den Spalten steht) die Häufigkeiten ins Verhältnis. Der Hauptunterschied ist aber, dass wir die Haustierkategorien (aq03 = 1-3) addieren müssen:

\[\text{Odds Haustier in 2P-HH} = \frac{153+250+43}{938} = 0.4754797\] \[\text{Odds Haustier allein} = \frac{41 +65 +9 }{579} = 0.1986183\] \[\text{Odds Ratio Haustier 2P-HH vs. allein} = \frac{0.4754797}{0.1986183} = 2.393937\] \[\text{Odds Ratio Haustier allein vs. 2P HH} = \frac{0.1986183}{0.4754797}=0.4177219\]

Interpretation:

• Allein lebende Befragte haben im Vergleich zu zweit lebenden Befragten die 0.418-fache Chance ein Haustier im Haushalt zu haben.
• Zu zweit lebende Befragte haben im Vergleich zu allein lebenden Befragten die 2.394-fache Chance ein Haustier im Haushalt zu haben.

\(\rightarrow\) Haben allein lebende Befragte eher Katzen als Befragte in einem Haushalt mit 4 Personen? (aq03 = 2 & 3 sind Katzenbesitzer*innen)²

5.3.2 Chi²-basierte Maße

\(\chi^2\) basiert auf dem Vergleich der beobachteten Häufigkeit mit einer (theoretischen) Verteilung, welche statistische Unabhängigkeit abbildet (Indifferenztabelle - mehr dazu). Wir bleiben bei aq03 und dh01. Den \(\chi^2\)-Wert für diese Häufigkeitstabelle bekommen wir mit , chi2:

tab aq03 dh04, chi

 HUND ODER KATZE |                                    ANZAHL DER HAUSHALTSPERSONEN
    IM HAUSHALT? |         1          2          3          4          5          6          7          8         10 |     Total
-----------------+---------------------------------------------------------------------------------------------------+----------
            HUND |        41        153         86         73         32          4          2          0          0 |       391 
           KATZE |        65        250        120         91         31          6          4          0          0 |       567 
          BEIDES |         9         43         29         26         11          5          1          0          1 |       125 
KEINS VON BEIDEN |       579        938        388        342         91         16          7          2          0 |     2,363 
-----------------+---------------------------------------------------------------------------------------------------+----------
           Total |       694      1,384        623        532        165         31         14          2          1 |     3,446 

         Pearson chi2(24) = 157.1103   Pr = 0.000

5.3.3 Cramer’s \(\upsilon\)

Auf Basis dieses \(\chi^2\)-Werts von 157.11 können wir Cramer’s \(\upsilon\) berechnen. Dieses ist definiert als der Quotient aus dem \(\chi^2\)-Wert und der Fallzahl multipliziert mit dem Minimum der Zeilen- und Spaltenzahl. n, erkennen wir aus dem Total rechts unten in der Tabelle. Außerdem hat unsere Tabelle 4 Zeilen und 10 Spalten, dementsprechend entspricht das Minimum hier 4:

\[ Cramer's\,\,\upsilon = \sqrt{\frac{\chi^2}{n*\,min(k-1,m-1)}}=\sqrt{\frac{157.1103}{3466*(4-1)}} = 0.01510967\]

Dieser Wert für Cramer’s \(\upsilon\) legt einen praktisch keinen Zusammenhang nahe.

dis sqrt(157.1103/(3466*3))

.12292138

5.3.4 \(\phi\)

Eine Variante von Cramer’s \(\upsilon\) für 2x2-Tabellen ist \(\phi\). Dies wäre das passende Maß für die zusammengefasste Variable aller Haustierbesitzer*innen aq03b von oben und dh01:

tab aq03b dh01, chi

           | MEHRPERSONENHAUSHALT?
     aq03b | MEHRPERSO  EINPERSON |     Total
-----------+----------------------+----------
         0 |       968        115 |     1,083 
         1 |     1,784        579 |     2,363 
-----------+----------------------+----------
     Total |     2,752        694 |     3,446 

          Pearson chi2(1) =  89.0092   Pr = 0.000

\[\phi= \sqrt{\frac{\chi^2}{n}}=\sqrt{\frac{89.0092}{3466}} = 0.1602\]

dis sqrt(89.0092/3466)

.16025189

---

Übung3

---

5.4 Welches Maß richtig?

Wir haben jetzt eine ganze Reihe an Zusammenhangsmaßen kennengelernt, die folgende Liste fasst nochmal alle Varianten zusammen. Es gibt noch eine ganze Reihe weiterer Zusammenhangsmaße und diese Liste deckt lediglich die Maße ab, die wir kennengelernt haben:

• nominal skalierte Variablen
  • Odds Ratio: basierend auf Kreuztabelle tab x y
  • \(\chi^2\)-basierte Maße tab x y, chi, danach Division von \(\chi^2\) durch n und Zahl der Spalten/Zeilen
• ordinal skalierte Variablen
  • Spearman-Rangkorrelationskoeffizient spearman x y
  • Konkordanzmaße
    • Kendall’s \(\tau_a\) & Kendall’s \(\tau_b\): ktau x y
    • Goodman & Kruskal’s \(\gamma\): tab x y, gamma
• metrische skalierte Variablen
  • Zusammenhangsstärke: Pearson-Korrelationskoeffizient corr x y
  • Regression zur Vorhersage von Werten auf Basis einer Variable: reg x y

Ausschlaggebend ist dabei die Variable mit dem niedrigeren Skalenniveau! Ggf. können metrische Variablen durch Kategorisierung (Kapitel 3) in ordinale Variablen überführt werden.

5.5 Übungen 5

5.5.1 Übung 5-1

1. Laden Sie den kumulierten Allbusdatensatz (Allbus_1980-2018.dta) in Stata und wählen Sie die Befragten aus dem Jahr 2014 aus! Untersuchen Sie den Zusammenhang zwischen dem Alter der Befragten age und der Dauer des Fernsehkonsums (lm02) in Minuten! Verwenden Sie age als unabhängige Variable.
   • Vergessen Sie nicht, die Missings mit mvdecode zu überschreiben oder mit keep/drop auszuschließen.
   • Überprüfen Sie z.B. mit summarize für beide Variablen, ob alle negativen Werte ausgeschlossen wurden.
   • Berechnen Sie das passende Zusammenhangsmaß!
   • Wie stark ist der Zusammenhang?
   • Welche Fernsehdauer würden Sie für eine*n 50-jährigen Befragte*n vorhersagen?
   • Welche Fernsehdauer würden Sie für eine*n 51-jährigen Befragte*n vorhersagen?
   • Welche Fernsehdauer würden Sie für eine*n 52-jährigen Befragte*n vorhersagen?
   • Vergleichen Sie diese drei Werte: was fällt Ihnen auf wenn Sie die vorhergesagten Werte vergleichen? (Tipp: bilden Sie die Differenz zwischen den Werten!)

Tipp: keep if year == 2014 wählt die Befragten aus dem Jahr 2014 aus

Zurück zu Zusammenhangsmaße für metrische Variablen

5.5.2 Übung 5-2

2. Laden Sie den kumulierten Allbusdatensatz (Allbus_1980-2018.dta) in Stata und wählen Sie die Befragten aus dem Jahr 2016 aus! Untersuchen Sie den Zusammenhang zwischen der Bildung der Befragten educ und ihrer Einstellung zur Erwerbstätigkeit von Müttern (fr03b)!
   • Vergessen Sie nicht, die Missings mit mvdecode zu überschreiben oder mit keep/drop auszuschließen. Schließen Sie auch 6 und 7 in educ als Missing aus!
   • Erstellen Sie eine Kontingenztabelle, um zu kontrollieren, ob alle negativen Werte ausgeschlossen wurden.
   • Berechnen Sie die passenden Zusammenhangsmaße!
   • Wie stark ist der Zusammenhang?
   • In welche Richtung deutet der Zusammenhang? Stimmen Befragte mit höherem Schulabschluss der Aussage eher zu oder eher nicht zu als Befragte mit niedrigeren Abschlüssen?

Hier die Frage zu fr03b aus dem Codebuch:

Zurück zu Zusammenhangsmaße für ordinale Variablen

5.5.3 Übung 5-3

3. Untersuchen Sie den Zusammenhang zwischen dem Geschlecht der Befragten (cf01) und deren Unsicherheitsgefühl (cf01)?
   • Verwenden Sie den Allbus2018.dta
   • Denken Sie daran, die Missings in cf01 auszuschließen
   • Berechnen Sie den Odds Ratio für Frauen sich nachts unsicher zu fühlen im Vergleich zu Männern!
   • Wie stark ist der Zusammenhang? Berechnen Sie das passende \(\chi^2\)-Maß!

Hier die Frage zu cf01 aus dem Codebuch:

Zurück zu Zusammenhangsmaße für nominale Variablen

5.5.4 Weitere Übungen 5

4. Gibt es einen Zusammenhang zwischen dem BMI (hs18) und dem Einkommen (inc) der Befragten aus dem Jahr 2014?
   • Laden Sie also den kumulierten Allbusdatensatz (Allbus_1980-2018.dta) in Stata und wählen Sie die Befragten aus dem Jahr 2014 aus.
   • Vergessen Sie nicht, die Missings mit mvdecode zu überschreiben.
   • Welches ist das passende Zusammenhangsmaß für diesen Zusammenhang?
   • Berechnen Sie dementsprechend die Zusammenhängsstärke!
5. Ist die Zustimmung zur Aussage “Ich bin stolz, ein Deutscher zu sein” in kleineren Orten größer? Berechnen Sie ein geeignetes Maß für den Zusammenhang zwischen gkpol und der entsprechenden Variable (px01)!
   • Berechnen Sie diesen Zusammenhang für das Jahr 2018! Laden Sie also den Allbus2018.dta
   • Welches Zusammenhangsmaß können Sie verwenden? (Zur Erinnerung: das niedrigere Skalenniveau ist ausschlaggebend!)
   • Berechnen Sie dementsprechend die Zusammenhängsstärke!

Hier die Frage zu px01 aus dem Codebuch:

6. Untersuchen Sie den Zusammenhang zwischen dem Wohnortgröße (gkpol) und dem Unsicherheitsgefühl (cf01) der befragten Frauen im Allbus2018.dta
   • Denken Sie daran, die Missings in cf01 auszuschließen
   • Berechnen Sie den Odds Ratio sich nachts unsicher zu fühlen für Bewohnerinnen aus Orten mit 5.000-19.999 Einwohnern im Vergleich im Vergleich zu Frauen aus Großstädten mit > 500.000 Einwohnern!
   • Wie stark ist der Zusammenhang zwischen gkpol und cf01 hier? Berechnen Sie das passende \(\chi^2\)-Maß!

5.6 Anhang

5.6.1 Idee einer Regression

Zum Einstieg betrachten wir zunächst einen (fiktiven) Datensatz mit lediglich 4 Fällen und lediglich zwei Variablen: var1 und var2:

use "https://github.com/filius23/Stata_Skript/raw/master/regression_bsp.dta", clear
list

  var1 var2
1    1    2
2    2    4
3    7    7
4    8    6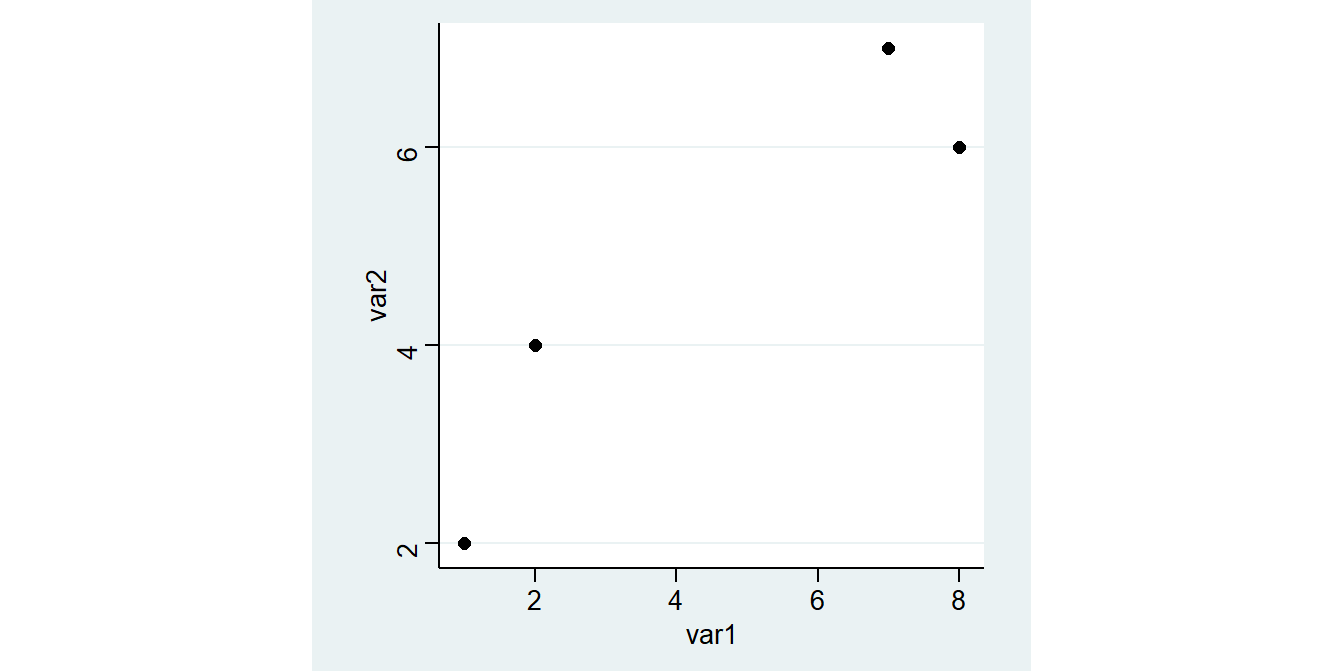

Ziel der Regression ist es, den Zusammenhang zwischen diesen beiden Variablen zu bestimmen. Gibt es einen Trend, in dem Sinn, dass ein höherer Wert von var1 mit einem höheren oder niedrigeren Wert von var2 einhergeht?

Etwas anders gesagt könnte man auch fragen, welchen Wert für var2 wir vorhersagen würden, wenn wir var1 kennen. Ein Ausgangspunkt ist das arithmetische Mittel. Dieses können wir mit mean zB für var2 berechnen.³ Diesen Wert fügen wir als neue Spalte mean_var2 in den Datensatz ein:

egen mean_var2 = mean(var2)
list

  var1 var2 mean_var2
1    1    2      4.75
2    2    4      4.75
3    7    7      4.75
4    8    6      4.75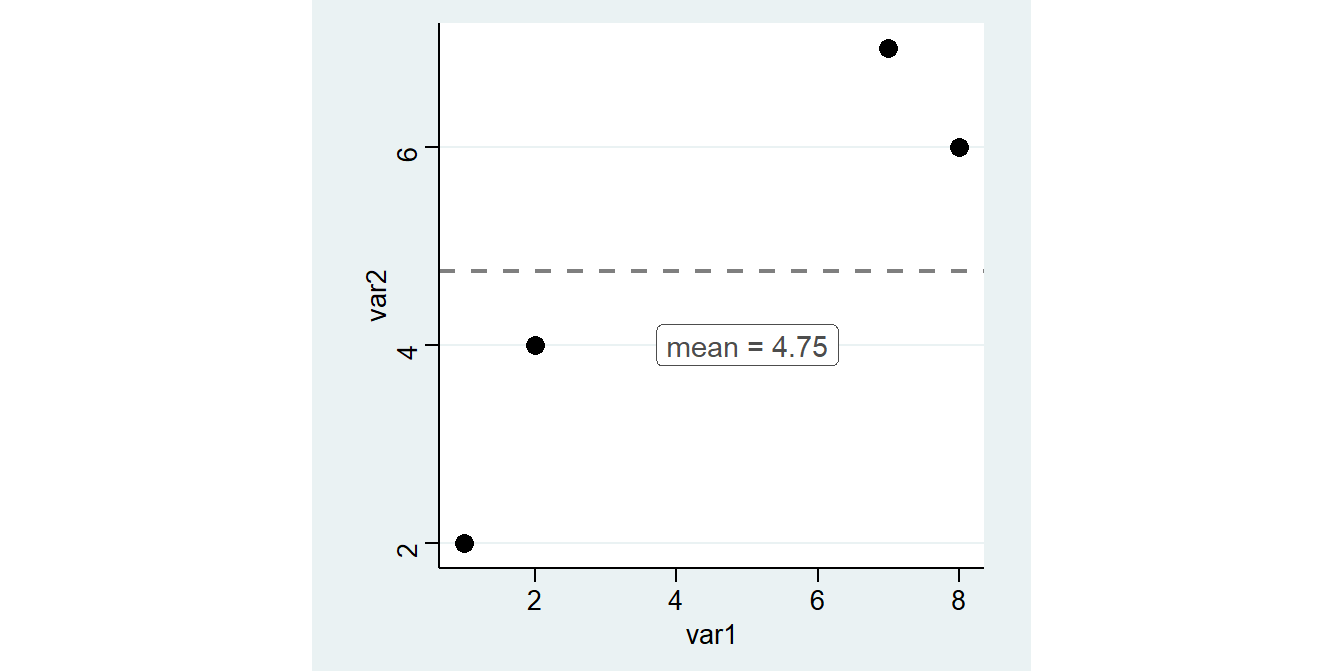

Müssten wir eine Prognose für die Werte von var2 abgeben, wäre das arith. Mittel eine gute Wahl. Die vorhergesagten Werte werden jeweils auf der Linie für das arith. Mittel liegen.

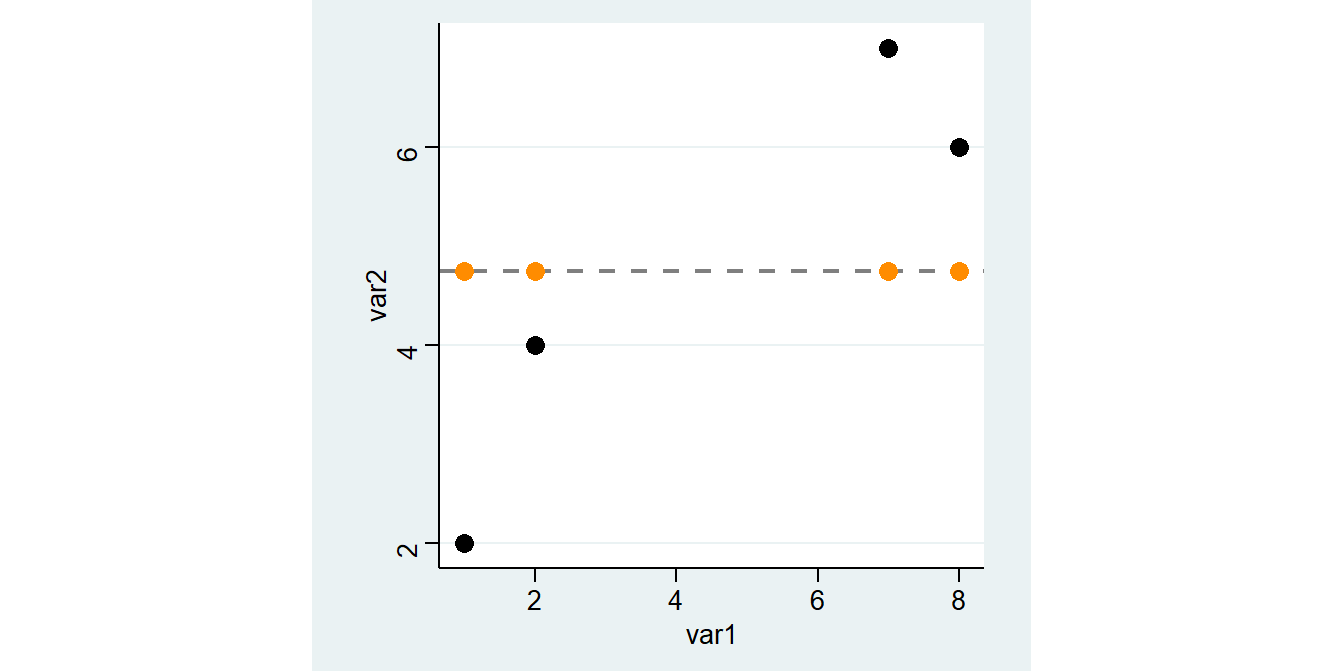
5.6.2 Residuen

Allerdings liegen wir mit dem arith. Mittel dann immer auch Stück daneben. Diese Abweichung zwischen dem tatsächlichen und dem vorhergesagten Wert wird als Residuum bezeichnet, in unserem Beispiel ist das jeweils die Differenz zwischen var2 und mean: \[Residuum = beobachteter\, Wert \; - \; vorhergesagter\,Wert\] Als Formel wird das in der Regel wie folgt dargestellt: \[\epsilon_{\text{i}} = \text{y}_{i} - \hat{\text{y}}_{i}\]

Wir können also die Residuen als Differenz zwischen var2 und mean berechnen und in df ablegen:

gen m_abw = var2 - mean_var2
list

  var1 var2 mean_var2 m_abw
1    1    2      4.75 -2.75
2    2    4      4.75 -0.75
3    7    7      4.75  2.25
4    8    6      4.75  1.25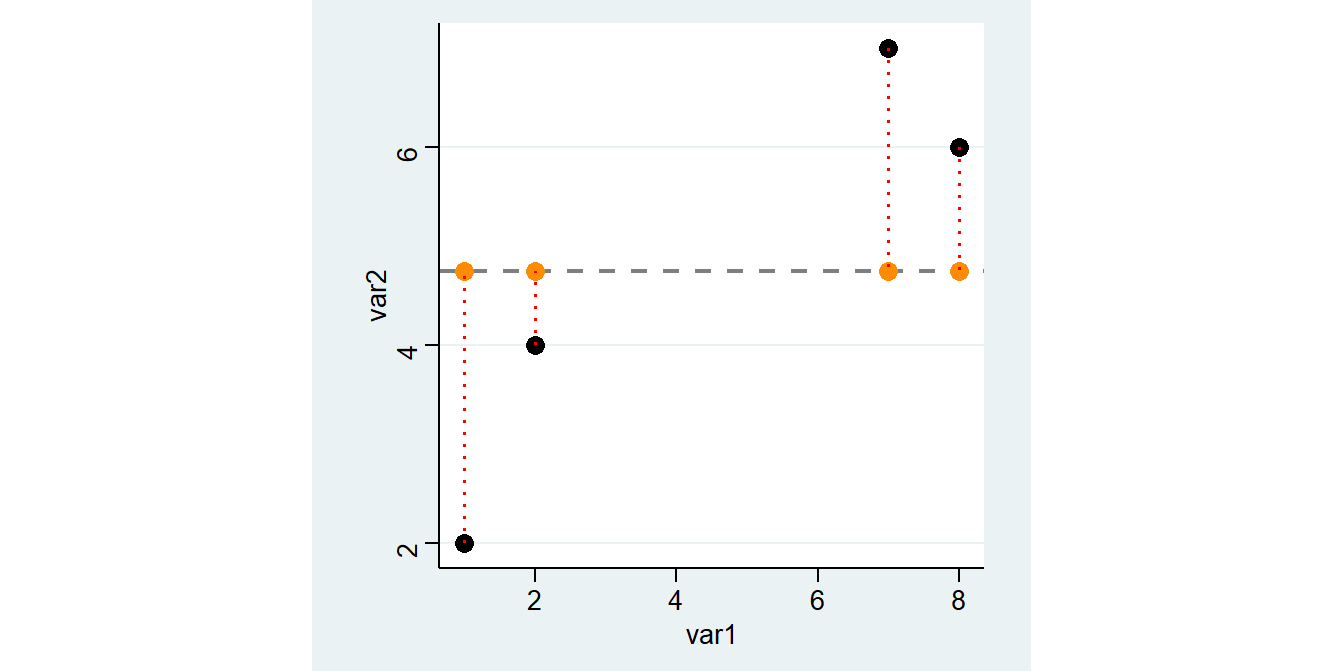

\(\rightarrow\) Was bedeutet also ein negativer oder ein positiver Wert für das Residuum?⁴

Die horizontale Linie für das arithm. Mittel ist aber sehr deutlich nicht die beste Methode, um die Werte für var2 vorherzusagen. In der Graphik können wir deutlich sehen, dass die Werte “weiter links”, also mit geringeren Werten für var1, auch geringere Werte für var2 aufweisen. Wir könnten also unseren Vorhersagefehler bzw. das Residuum minimieren indem wir die Linie drehen. Die Idee der Regressionsanalyse ist es dabei, die Residuuen zu minimieren. Was würde aber passieren wenn wir die Residuen aus der Mittelwertsvorhersage aufsummieren, um Sie dann zu minimieren?

5.6.3 Quadrierte Residuen

Mit tabstat ..., s(sum) können wir die Summe für eine Variable bilden:

list

  var1 var2 mean_var2 m_abw
1    1    2      4.75 -2.75
2    2    4      4.75 -0.75
3    7    7      4.75  2.25
4    8    6      4.75  1.25

tabstat m_abw, s(sum)

    variable |       sum
-------------+----------
       m_abw |         0
------------------------

Die Summe der Resiuden auf Basis des arith. Mittels ist immer Null!
Anders formuliert: die gestrichelten Linien nach oben sind in Summe genauso lang wie gestrichelten Linien nach unten. Die Lösung ist die Residuen zu quadrieren. So ergibt sich eine Kennzahl, die wir minimieren können:

gen m_abw2 = m_abw^2 
tabstat m_abw2, s(sum)

      Source |       SS       df       MS              Number of obs =       4
-------------+------------------------------           F(  1,     2) =   11.07
       Model |  12.4932432     1  12.4932432           Prob > F      =  0.0797
    Residual |  2.25675676     2  1.12837838           R-squared     =  0.8470
-------------+------------------------------           Adj R-squared =  0.7705
       Total |       14.75     3  4.91666667           Root MSE      =  1.0623

------------------------------------------------------------------------------
        var2 |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        var1 |   .5810811   .1746331     3.33   0.080    -.1703044    1.332467
       _cons |   2.135135   .9485004     2.25   0.153    -1.945933    6.216203
------------------------------------------------------------------------------

    variable |       sum
-------------+----------
      m_abw2 |     14.75
------------------------

  var1 var2 mean_var2 m_abw m_abw2
1    1    2      4.75 -2.75 7.5625
2    2    4      4.75 -0.75 0.5625
3    7    7      4.75  2.25 5.0625
4    8    6      4.75  1.25 1.5625

5.6.4 Interpretation der Regression

Die Minimierung erledigt reg für uns. Hier geben wir zuerst das Merkmal an, das auf der y-Achse liegt (die abhängige Variable) und dann das Merkmal für die x-Achse (unabhängige Variable) an. Ein positiver Wert unter Coef. in der Zeile von var1 bedeutet, dass unsere Gerade von links nach rechts ansteigt und ein negativer eine fallende Linie bedeuten würde. Der Wert unter var1 gibt an, um wieviel sich die Gerade pro “Schritt nach rechts” nach oben/unten verändert. Die Gerade steigt also pro Einheit von var1 um 0.5810811:

reg var2 var1

      Source |       SS       df       MS              Number of obs =       4
-------------+------------------------------           F(  1,     2) =   11.07
       Model |  12.4932432     1  12.4932432           Prob > F      =  0.0797
    Residual |  2.25675676     2  1.12837838           R-squared     =  0.8470
-------------+------------------------------           Adj R-squared =  0.7705
       Total |       14.75     3  4.91666667           Root MSE      =  1.0623

------------------------------------------------------------------------------
        var2 |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        var1 |   .5810811   .1746331     3.33   0.080    -.1703044    1.332467
       _cons |   2.135135   .9485004     2.25   0.153    -1.945933    6.216203
------------------------------------------------------------------------------

In unserer Grafik sieht diese Gerade so aus:

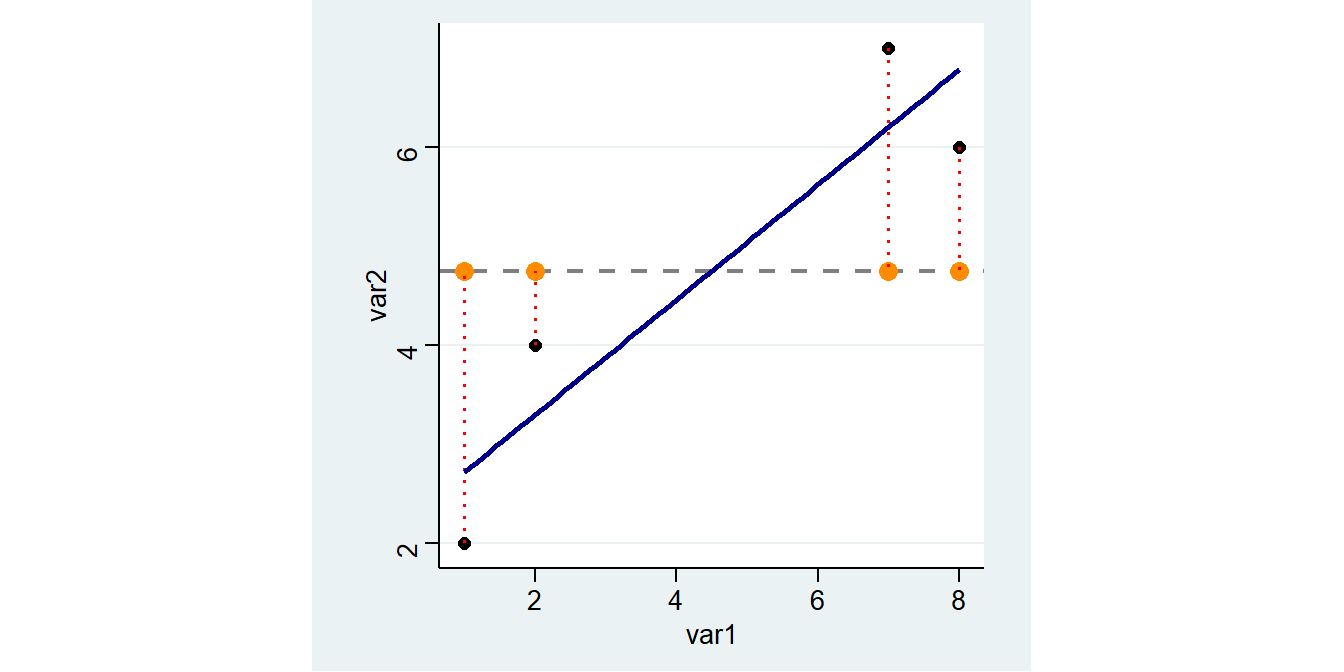
5.6.5 Vorhergesagte Werte

Wie hoch ist nun der vorhergesagte Wert auf Basis der blauen Gerade? Die vohergesagten Werte aus reg var2 var1 entsprechen einfach der Summe aus dem Wert neben _cons und dem Koeffizienten neben var1 multipliziert mit dem jeweiligen Wert für var1.⁵

reg var2 var1, noheader

        var2 |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        var1 |   .5810811   .1746331     3.33   0.080    -.1703044    1.332467
       _cons |   2.135135   .9485004     2.25   0.153    -1.945933    6.216203
------------------------------------------------------------------------------

Vorhergesagte Werte werden mit \(\widehat{var2}\) bezeichnet - der ^ steht dabei für “vorhergesagt”:

\[\widehat{var2}=\texttt{Intercept} + 0.5811 \times \texttt{var1}\]
Für die erste Zeile ergibt sich also folgender vorhergesagter Wert: 2.1351+0.5811*1= 2.7162

Also könnten wir mit gen die vorhergesagten Werte “manuell” berechnen:

gen manual_vorhers = 2.1351 + 0.5811 * var1

Die vorhergesagten Werte können wir auch mit predict berechnen und in einer neuen Variable pred_vorher ablegen:

predict pred_vorher, xb

  var1 var2 mean_var2 m_abw m_abw2 manual_vorhers pred_vorher
1    1    2      4.75 -2.75 7.5625         2.7162    2.716216
2    2    4      4.75 -0.75 0.5625         3.2973    3.297297
3    7    7      4.75  2.25 5.0625         6.2028    6.202703
4    8    6      4.75  1.25 1.5625         6.7839    6.783784

Die Grafik zeigt wie Vorhersagen auf Basis des Regressionsmodells aussehen: Sie entsprechen den Werten auf der blauen Geraden (der sog. Regressionsgeraden) an den jeweiligen Stellen für var1. 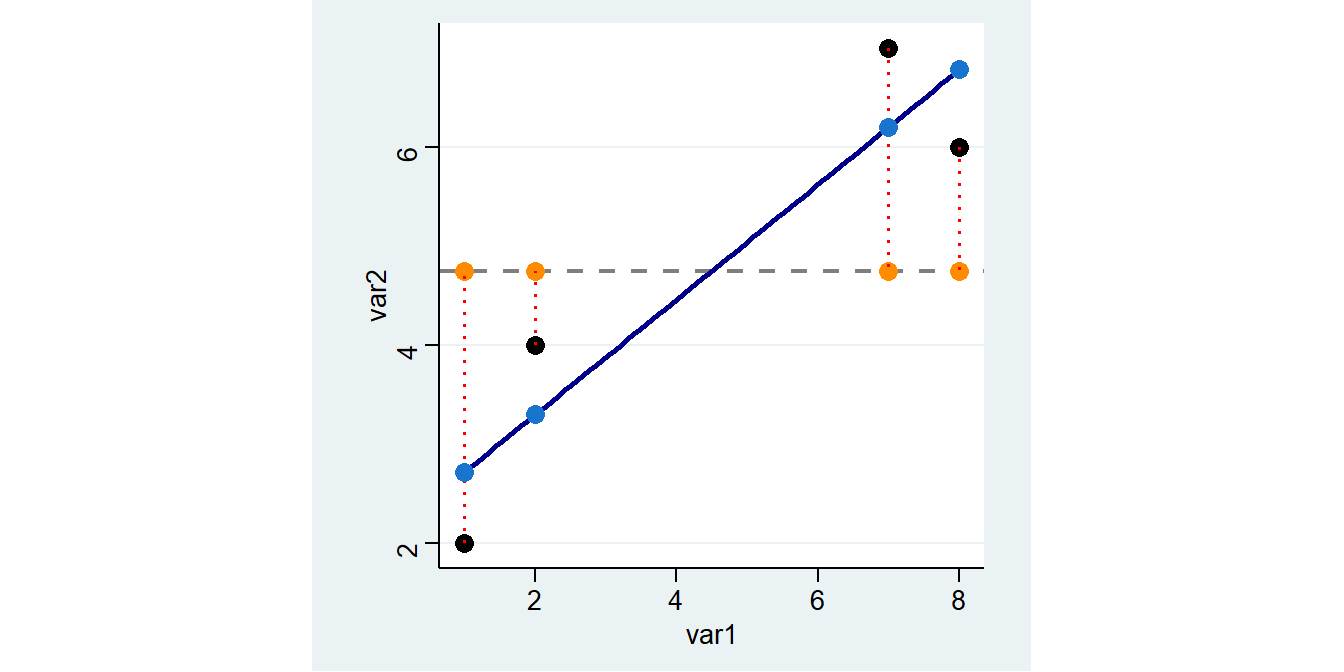Wir können erkennen, dass die hellblauen Punkte (also die Vorhersagen des Regressionsmodells) deutlich näher an den tatsächlichen Punkten liegen als die orangen Vorhersagen auf Basis des mean.

5.6.6 Residuen Teil 2

Trotzdem sind auch die hellblauen Punkte nicht deckungsgleich mit den tatsächlichen Werten. Es gibt also auch hier wieder Residuen, also Abweichungen des beobachteten vom vorhergesagten Wert. Wir können diese per Hand berechnen als Differenz zwischen dem tatsächlichen und dem vorhergesagten Wert:

gen res = var2 - pred_vorher 

Oder wir können Sie mit predict neue_variable , residuals erstellen:

reg var2 var1 // zunächst nochmal die regression laufen lassen
predict p_res , residuals
list

  var1 var2 mean_var2 m_abw m_abw2 manual_vorhers pred_vorher        res      p_res
1    1    2      4.75 -2.75 7.5625         2.7162    2.716216 -0.7162162 -0.7162162
2    2    4      4.75 -0.75 0.5625         3.2973    3.297297  0.7027027  0.7027027
3    7    7      4.75  2.25 5.0625         6.2028    6.202703  0.7972973  0.7972973
4    8    6      4.75  1.25 1.5625         6.7839    6.783784 -0.7837838 -0.7837838

Hier sind die Residuen für p_res als hellblaue Linien eingezeichnet: 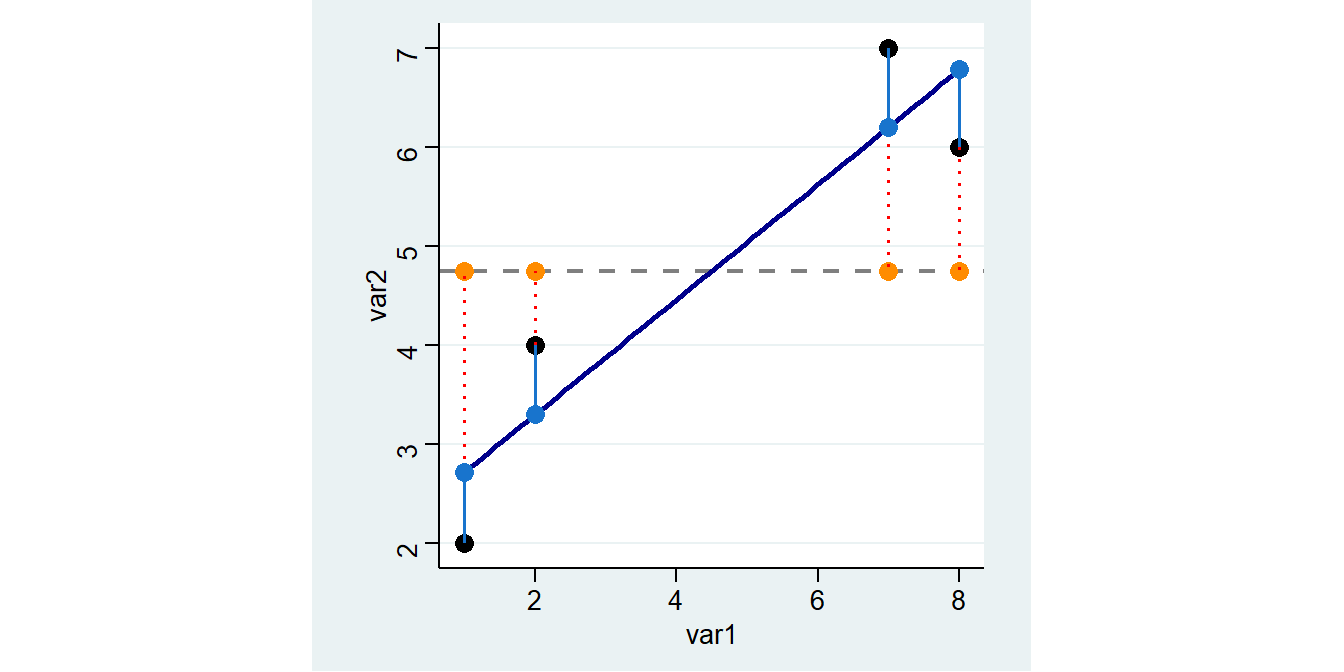\(\rightarrow\) Wie groß ist die (einfache) Summe der Residuen für pred_vorher?⁶

5.6.7 Modellgüte

Um zu beurteilen, um wieviel besser unsere Gerade aus reg die Werte vorhersagen kann als der mean können wir die Summe der quadrierten Residuen vergleichen. Dazu quadrieren wir also die Residuen:

gen res2 = res^2
list

  var1 var2 mean_var2 m_abw m_abw2 manual_vorhers pred_vorher        res      res2
1    1    2      4.75 -2.75 7.5625         2.7162    2.716216 -0.7162162 0.5129657
2    2    4      4.75 -0.75 0.5625         3.2973    3.297297  0.7027027 0.4937911
3    7    7      4.75  2.25 5.0625         6.2028    6.202703  0.7972973 0.6356830
4    8    6      4.75  1.25 1.5625         6.7839    6.783784 -0.7837838 0.6143170

Dann können wir die Summen der quadierten Abweichungen aus der Mittelwertregel und dem Regressionsmodell vergleichen:

dis 7.5625+0.5625+5.0625+1.5625 // abw2 aus Mittelwertsregel
14.75

dis 0.5129657+0.4937911+0.6356830+0.6143170 // res2 aus regressionsmodell
2.2567568

Zum Beispiel können wir uns fragen, um wieviel sich die Summe der quadrierten Residuen verringert wenn wir statt des mean unser reg-Modell verwenden:

dis 14.75 -  2.256757
12.493243

Wenn wir diese Veränderung ins Verhältnis mit dem “Ausgangswert”, also den Residuen aus der Mittelwertregel setzen, dann erhalten wir das \(R^{2}\) für unser reg-Modell. Dieses gibt die prozentuale Verringerung der Residuen durch das reg-Modell im Vergleich zur Mittelwertregel an:

dis (14.75 -  2.256757) / 14.75

.84699953

Unser Regressionsmodell kann also 84,7% der Streuung um den Mittelwert erklären. Dieser Wert wird auch als \(R^2\) bezeichnet. Im Regressionsoutput können wir das \(R^2\) oben rechts unter R-squared ablesen.

reg var2 var1

      Source |       SS       df       MS              Number of obs =       4
-------------+------------------------------           F(  1,     2) =   11.07
       Model |  12.4932432     1  12.4932432           Prob > F      =  0.0797
    Residual |  2.25675676     2  1.12837838           R-squared     =  0.8470
-------------+------------------------------           Adj R-squared =  0.7705
       Total |       14.75     3  4.91666667           Root MSE      =  1.0623

------------------------------------------------------------------------------
        var2 |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        var1 |   .5810811   .1746331     3.33   0.080    -.1703044    1.332467
       _cons |   2.135135   .9485004     2.25   0.153    -1.945933    6.216203
------------------------------------------------------------------------------

Außerdem sehen wir oben links in der Spalte SS die “Sum of Squares”. Hier finden wir auch die Werte von oben wieder: unter Total ist die Summe der quadrierten Abweichungen der beobachteten Werte vom arith. Mittel angegeben (14.75, sozusagen die Summe der m_abw2 von oben). Residual gibt die Summe der Abweichungsquadrate zwischen den beobachteten Werten und den vorhergesagten Werten der Regression (2.256.., Die Summe von res2).

5.6.8 Indifferenztabelle

\(\chi^2\) ergibt sich wie gesagt aus der Differenz zwischen der Indifferenztabelle und den beobachteten Häufigkeiten. Die Indifferenztabelle können wir mit ,expected aufrufen (mit nofreq blenden wir die tatsächlichen Häufigkeiten aus):

tab  aq03  dh01, expected nofreq

 HUND ODER KATZE | MEHRPERSONENHAUSHALT?
    IM HAUSHALT? | MEHRPERSO  EINPERSON |     Total
-----------------+----------------------+----------
            HUND |     312.3       78.7 |     391.0 
           KATZE |     452.8      114.2 |     567.0 
          BEIDES |      99.8       25.2 |     125.0 
KEINS VON BEIDEN |   1,887.1      475.9 |   2,363.0 
-----------------+----------------------+----------
           Total |   2,752.0      694.0 |   3,446.0 

Ausgangspunkt für diese Indifferenztabelle sind die relativen Häufigkeiten der tatsächlich beoachteten Werte:

tab  aq03  dh01, cell nofreq

 HUND ODER KATZE | MEHRPERSONENHAUSHALT?
    IM HAUSHALT? | MEHRPERSO  EINPERSON |     Total
-----------------+----------------------+----------
            HUND |     10.16       1.19 |     11.35 
           KATZE |     14.57       1.89 |     16.45 
          BEIDES |      3.37       0.26 |      3.63 
KEINS VON BEIDEN |     51.77      16.80 |     68.57 
-----------------+----------------------+----------
           Total |     79.86      20.14 |    100.00 

0.26 % der Befragten wohnen alleine (dh01 = 2) und haben einen Hund und eine Katze (aq03=3).
Uns interessieren hier nur die Randverteilungen aus Sum: 3.63 % der Befragten haben einen Hund und eine Katze (aq03=3). 20.14 % der Befragten wohnen alleine (dh01 = 2).

	MEHRPERSO	EINPERSON	Total
HUND	A	E	0.1135
KATZE	B	F	0.1645
BEIDES	C	G	0.0363
KEINES VON BEIDEM	D	H	0.6857
Total	0.7986	0.2014	1

Wären beide Merkmale unabhängig voneinander, würden wir erwarten, dass die Wahrscheinlichkeit für das Auftreten einer Merkmalskombination dem Produkt der Einzelwahrscheinlichkeiten entspricht (das ist die “Indifferenz”): \(P(A\cup B) = P(A) \times P(B)\). Bspw. ergibt sich der erwartete Wert für die Zellen dann aus der relativen Randverteilung multipliziert mit der Gesamtfallzahl:

• für Zelle B: 0.1645 \(\times\) 0.7986 \(\times\) 3446 = 452.8102.

• für Zelle C: 0.0363 \(\times\) 0.7986 \(\times\) 3446 = 99.8259.

• für Zelle H: 0.6857 \(\times\) 0.2014 \(\times\) 3446 = 475.8915.

Dies sind auch die Werte, die Stata uns oben mit tab aq03 dh01, expected nofreq ausgegeben hatte.

\(\chi^2\) ist dann die summierte Differenz zwischen dieser Indifferenztabelle (also der erwarteten Verteilung bei Unabhängigkeit beider Merkmale) und den beobachteten Häufigkeiten: je größer die Differenz, desto unwahrscheinlicher ist es, dass beide Merkmale unabhängig sind.

---

1. 579 Personen leben allein und ohne Haustier.↩︎

2. Nein - weil \(\text{Odds Haustier in 4P-HH} = \frac{73+91+26}{342} = 0.5555556\) und \(\text{Odds Haustier allein} = \frac{41 +65 +9 }{579} = 0.1986183\), dementsprechend \(\text{Odds Ratio Haustier allein vs. 4P HH} = \frac{0.1986183}{0.5555556}=0.3575129\)↩︎

3. Mehr zu egen in Kapitel 11.4↩︎

4. Ein positiver Wert des Residuums bedeutet, dass der beobachtete Wert größer als der vorhergesagte Wert ist. Die Regressionsgerade unterschätzt also den Wert. Ein negatives Residuum bedeutet dementsprechend, dass die Regressionsgerade den Wert überschätzt - der wahre Wert ist niedriger als der vorhergesagte Wert. Siehe Formeln↩︎

5. Die Option noheader macht den Output von reg etwas übersichtlicher.↩︎

6. Die (einfache, unquadrierte) Summe der Resiuden beträgt auch hier Null.↩︎