9 Weitere Hypothesentests

9.1 Vergleich von Varianzen mit dem F-Test

Um die Varianzen zweier Stichproben zu überprüfen, steht uns der F-Test zur Verfügung - in Stata mit sdtest. Getestet wird beim F-Test die Hypothese, dass die Varianzen zweier Grundgesamtheiten gleich oder ungleich (zweiseitiger Test) sind bzw. dass die Varianz der einen Grundgesamtheit größer ist als die der anderen (einseitiger Test).

Der F-Test hat einige Voraussetzungen:

  • Die Variablen sind (mind.) intervallskaliert
  • Die Variablen sind in der Grundgesamtheit (annähernd) normalverteilt
  • Die zu vergleichenden Gruppen sind voneinander unabhängig (unverbundene Stichproben)

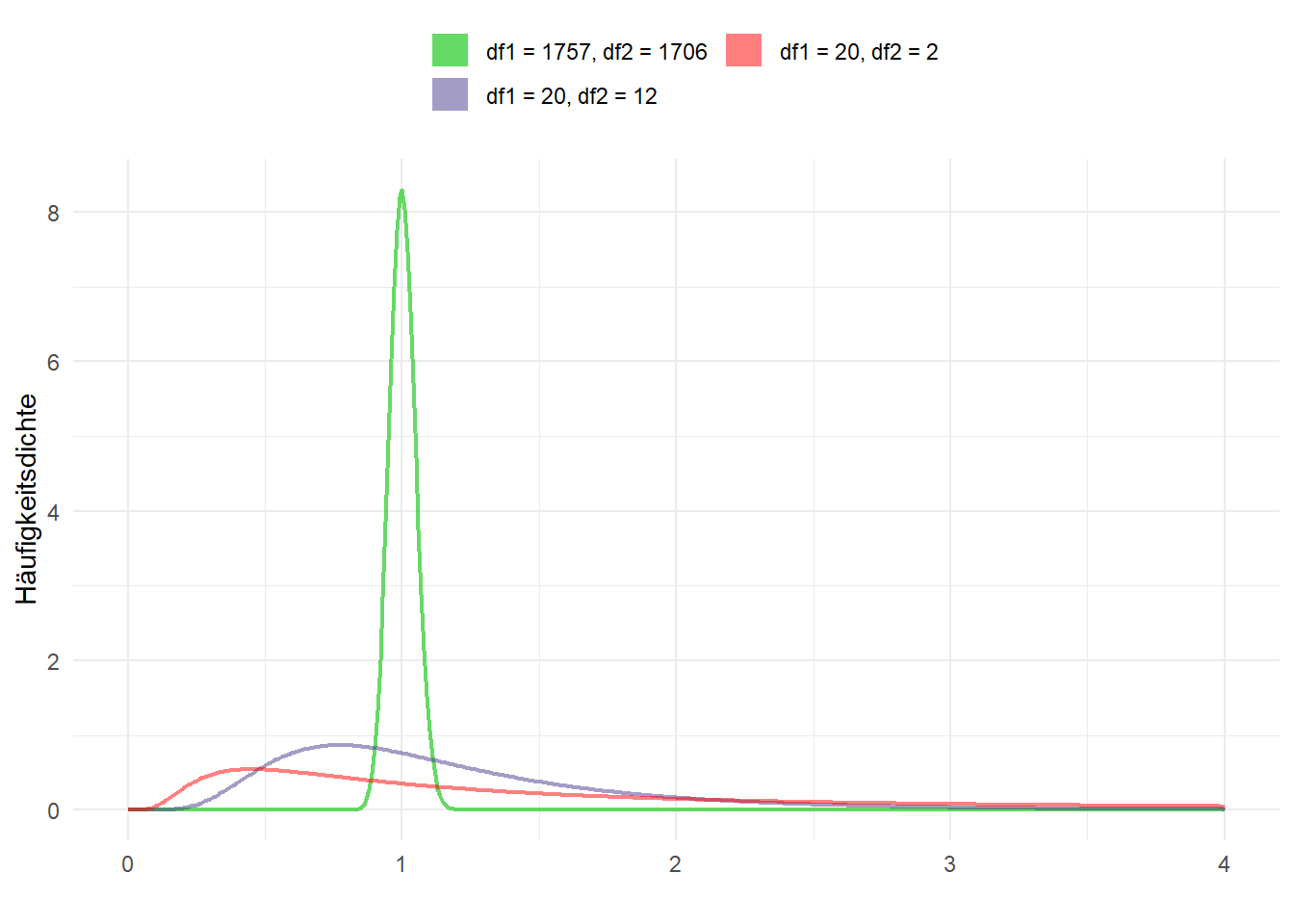
Es gibt also auch hier wieder gerichtete und ungerichtete Hypothesen. Da allerdings die F-Verteilung nicht symmetrisch ist, wird nur rechtsseitig getestet. Daher sollte beim Test die größere Varianz immer im Zähler stehen.

  • ungerichtete/beidseitige Hypothese:

\(\qquad H_0: \frac{\sigma^{2}_{1}}{\sigma^{2}_{2}} = 1 \qquad H_A: \frac{\sigma^{2}_{1}}{\sigma^{2}_{2}} \neq 1 \qquad \qquad \Rightarrow H_A:\;\sigma^{2}_{1} \neq \sigma^{2}_{2}\)

  • rechtsseitige Hypothese:

\(\qquad H_0: \frac{\sigma^{2}_{1}}{\sigma^{2}_{2}} \leqslant 1 \qquad H_A: \frac{\sigma^{2}_{1}}{\sigma^{2}_{2}} > 1 \qquad \qquad \Rightarrow H_A:\;\sigma^{2}_{1}>\sigma^{2}_{2}\)

Wie schon beim t-Test geht es bei den Hypothesen um die Grundgesamtheit. Daher wird hier der griechische Buchstabe für die Varianz, \(\sigma^2\), verwendet. Da wir i.d.R. keine Angabe zur Varianz der Grundgesamtheiten vorliegen haben, wird beim F-Test auf die Stichprobenvarianzen (\(s^2\)) zurückgegriffen. Der Quotient der Varianzen ist F-verteilt. Somit berechnet sich die F-Statistik aus dem Quotienten der beiden Stichprobenvarianzen, wobei – nochmal – die größere Varianz im Zähler steht: \[F = \frac{s^{2}_{1}}{s^{2}_{2}}\] Wir kommen nochmal auf das Beispiel der Körpergrößen aus dem Allbus 2014 aus Session 8 zurück und fragen uns, ob die Varianz der Körpergröße sich bei Männern und Frauen unterscheidet:

cd "..."
use  "Allbus_1980-2018.dta",clear
keep  if year == 2014 & hs16 > 0

Im konkreten Fall ist also \(s^{2}_{Maenner}\) der Schätzer für \(\sigma^{2}_{Manner}\) und \(s^{2}_{Frauen}\) der Schätzer für die \(\sigma^{2}_{Frauen}\). Wir berechnen also zunächst die Stichprobenvarianzen:

tabstat hs16, s(var cv) by(sex)
Summary for variables: hs16
     by categories of: sex (GESCHLECHT, BEFRAGTE(R))

   sex |  variance        cv
-------+--------------------
  MANN |  51.55268  .0401752
  FRAU |  42.40775  .0392561
-------+--------------------
 Total |  88.18758   .054472
----------------------------

Wir haben Glück - die Gruppe mit der größeren Stichprobenvarianz hat auch den kleineren Zahlenwert zugewiesen (Männer haben bei sex die 1). Wir können also sdtest ohne Umwege anwenden.1

In sdtest() geben wir zunächst die zu testende Variable an, dann die Gruppierungsvariable:

sdtest hs16, by(sex)
Variance ratio test
------------------------------------------------------------------------------
   Group |     Obs        Mean    Std. Err.   Std. Dev.   [95% Conf. Interval]
---------+--------------------------------------------------------------------
    MANN |    1758    178.7179    .1712443     7.18002     178.382    179.0537
    FRAU |    1707    165.8881     .157618    6.512124     165.579    166.1973
---------+--------------------------------------------------------------------
combined |    3465    172.3974    .1595336    9.390824    172.0846    172.7102
------------------------------------------------------------------------------
    ratio = sd(MANN) / sd(FRAU)                                   f =   1.2156
Ho: ratio = 1                                  degrees of freedom = 1757, 1706

    Ha: ratio < 1               Ha: ratio != 1                 Ha: ratio > 1
  Pr(F < f) = 1.0000         2*Pr(F > f) = 0.0000           Pr(F > f) = 0.0000

Da der p-Wert für den beidseitigen Test (mittlere Spalte, unter Ha: ratio != 1) deutlich unter 0,05 liegt wird die \(H_0\) verworfen und wir gehen von ungleichen Varianzen bei den Körpergrößen von Männern und Frauen aus.

Außerdem kann die \(H_0: \frac{\sigma^{2}_{1}}{\sigma^{2}_{2}} \leqslant 1\) verworfen werden (letzte Spalte, unter Ha: ratio > 1). D.h. die Varianz der Körpergröße von Männern ist signifikant größer als die Varianz der Körpergröße bei Frauen.

Übung1

9.2 Proportionen und Häufigkeiten

9.2.1 Binomialtest

Für dichtome abhängige Variablen eignet sich der Binomialtest. Wir können mit dem Binomialtest testen, ob ein Anteil eines Merkmals sich signifikant von einem Wert unterscheidet. Dieser Anteil wird als \(\pi\) bezeichnet und beschreibt Auftrittswahrscheinlichkeit des interessierenden Merkmals in der Grundgesamtheit. In R können wir den Binomialtest mit binom.test aufrufen. Auch hier gibt es wieder gerichtete und ungerichtete Hypothesen:

  • ungerichtete/beidseitige Hypothese: \(H_0: \pi = p \qquad H_A: \pi \neq p\)

  • linksseitige Hypothese:
    \(H_0: \pi \geqslant p \qquad H_A: \pi < p\)

  • rechtssseitige Hypothese:
    \(H_0: \pi \leqslant p \qquad H_A: \pi > p\)

Wir könnten uns zB. fragen ob der Anteil der Befragten ohne Haustier im Allbus 2014 sich von \(67\%\) unterscheidet. Dazu wählen wir zunächst alle Befragten des Allbus 2014 aus, welche die Frage nach den Haustieren (aq03) beantwortet haben (aq < 0 sind missings, daher verwenden wir schlicht aq03 > 0). Dazu erstellen wir aus aq03 noch eine Dummyvariable, welche 1 für das interessierende Merkmal (kein Haustierbesitz) und 0 in allen anderen Fällen annimmt:

cd ""
use  "Allbus_1980-2018.dta",clear
keep  if year == 2014 & aq03>0
gen pet = (aq03 == 4)
tab aq03 pet
 HUND ODER KATZE |          pet
    IM HAUSHALT? |         0          1 |     Total
-----------------+----------------------+----------
            HUND |       397          0 |       397 
           KATZE |       569          0 |       569 
          BEIDES |       127          0 |       127 
KEINS VON BEIDEN |         0      2,374 |     2,374 
-----------------+----------------------+----------
           Total |     1,093      2,374 |     3,467

Mit bitest können wir dann den Binomialtest durchführen, dazu geben wir neben der Variable pet den zu testenden Wert als Dezimalwert an. Stata interpretiert dabei die Ausprägung 1 als “Treffer” und 0 als “Nicht-Treffer”, daher haben wir eben die interessierende Ausprägung (kein Haustier) als 1 in pet definiert.

bitest pet == .67
    Variable |        N   Observed k   Expected k   Assumed p   Observed p
-------------+------------------------------------------------------------
         pet |     3467       2374      2322.89       0.67000      0.68474

  Pr(k >= 2374)              = 0.033408  (one-sided test)
  Pr(k <= 2374)              = 0.969210  (one-sided test)
  Pr(k <= 2271 or k >= 2374) = 0.065472  (two-sided test)

Der rechtsseitige Test (erste Zeile) ergibt, dass der Anteil der Befragten ohne Haustier signifikant größer als 67% ist. Der linksseitige Test (zweite Zeile) ergibt, dass der Anteil der Befragten ohne Haustier nicht signifikant kleiner als 67% ist. Außerdem können wir auf Basis des beidseitigen Tests (letzte Zeile) die \(H_0: \pi = .67\) nicht verwerfen, da der p-Wert größer 0,05 ist. Der Anteil der Befragten ohne Haustier unterscheidet sich also nicht signifikant von 67%.

Übung 2

9.2.2 Chi²-Test

Häufig ist aber auch für dichtome Merkmale von Interesse, ob sich die Auftrittswahrscheinlichkeit zwischen zwei Gruppen unterscheidet. Hierfür eignet sich der \(\chi^{2}\)-Test. Der \(\chi^{2}\)-Test testet, ob sich die beobachteten absoluten Häufigkeiten signifikant von den absoluten Häufigkeiten unterscheiden, die wir erwarten würden wenn beide Merkmale unabhängig voneinander sind. Die Differenz zwischen der beobachteten und der erwarteten absoluten Häufigkeit ergibt den \(\chi^{2}\)-Wert. Ist \(\chi^{2} \approx 0\), dann können wir davon ausgehen, dass die beiden Merkmale unabhängig voneinander sind. Ist \(\chi^{2}\) aber größer Null, so gehen wir von einem Zusammenhang aus. Beim \(\chi^{2}\)-Test geht die \(H_0\) davon aus, dass es keinen Zusammenhang gibt. Die \(H_{A}\) besagt hingegen, dass einen Zusammenhang zwischen den beiden untersuchten Merkmalen besteht.

\(H_{0}: \chi^2 = 0 \qquad H_A: \chi^2 > 0\)

Den \(\chi^2\)-Test erhalten wir, indem wir mit tabulate eine Kontingenztabelle erstellen und die Option chi angeben. Beispielsweise könnten wir untersuchen, ob es einen Zusammenhang zwischen dem Geschlecht der Befragten und dem Haustierbesitz gibt:

tab sex pet, chi
 HUND ODER KATZE |          pet
    IM HAUSHALT? |         0          1 |     Total
-----------------+----------------------+----------
            HUND |       397          0 |       397 
           KATZE |       569          0 |       569 
          BEIDES |       127          0 |       127 
KEINS VON BEIDEN |         0      2,374 |     2,374 
-----------------+----------------------+----------
           Total |     1,093      2,374 |     3,467 

          Pearson chi2(3) =  3.5e+03   Pr = 0.000

Da der p-Wert deutlich unter 0,05 liegt, können wir davon ausgehen, dass es in der Grundgesamtheit einen Zusammenhang zwischen dem Geschlecht der Befragten und dem Haustierbesitz gibt.

9.3 Überblick

In allen Tests (außer \(\chi^2\)) können beidseitige, linksseitige oder rechtsseitige Hypothesen untersucht werden.

  • Mittelwertvergleich: ttest

    • Vergleich zu einem Referenzwert: ttest testvariable == referenzwert

    Zudem gibt es bein Mittelwertvergleichen insgesamt zwei Aspekte, anhand derer sich t-Tests allgemein unterscheiden:

    • Die Varianz der Messwerte in den verglichenen Gruppen ist …
      • gleich: \(\Rightarrow\) ttest testvariable, by(gruppenvariable)
      • verschieden: \(\Rightarrow\) ttest testvariable, by(gruppenvariable) unequal
    • Verbundene oder unverbundene Stichprobe?
      • Sind die einzelnen Messwerte voneinander unabhängig? D.h. ein Messwert steht in keinem direkten Zusammenhang mit einem anderen \(\Rightarrow\) ttest testvariable, by(gruppenvariable) für eine unverbundene Stichprobe (mit ggf. unequal)
      • Stehen die einzelnen Messwerte in einem Zusammenhang? D.h. ein Messwert steht in einem direkten Zusammenhang mit einem anderen \(\Rightarrow\) Werte für beide Variablen sollten “nebeneinander” abgelegt sein (wide-Format), dann kann mit ttest vorher==nachher ein verbundener ttest durchgeführt werden.

  • Varianzvergleich,unterscheidet sich die Varianz zwischen zwei Gruppen?

    • sdtest testvariable, by(gruppenvariable)

  • Anteile vergleichen:

    • mit einem behaupteten Wert: bitest testvariable == referenzwert
    • zwischen Gruppen: Kreuztabelle erstellen und mit tab var1 var2, chi Unabhängigkeit testen

9.4 Signifikanz in Regressionen

Wir hatten uns in Session 5 u.a. Regressionsmodelle angesehen:

cd D:\oCloud\Home-Cloud\Lehre\Methodenseminar
use "Allbus_1980-2018.dta", clear
keep if year == 2014
mvdecode lm02 age, mv(-32/-1)
reg lm02 age
      Source |       SS       df       MS              Number of obs =    3363
-------------+------------------------------           F(  1,  3361) =  176.96
       Model |  1389413.03     1  1389413.03           Prob > F      =  0.0000
    Residual |  26388575.7  3361  7851.40605           R-squared     =  0.0500
-------------+------------------------------           Adj R-squared =  0.0497
       Total |  27777988.8  3362  8262.34051           Root MSE      =  88.608

------------------------------------------------------------------------------
        lm02 |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
         age |    1.16511   .0875841    13.30   0.000     .9933869    1.336834
       _cons |   95.58535   4.611489    20.73   0.000     86.54374     104.627
------------------------------------------------------------------------------

In der Spalte P>|t| und t sehen wir die Ergebnisse eines t-Tests für die jeweiligen Koeffizienten. Hier wird der Koeffizient (sprich: die Steigung der Geraden) “gegen Null” getestet. Ist der Zusammenhang zwischen dem Alter der Befragten und ihrem Fernsehkonsum in der Population nicht eigentlich 0?

\[H_0:\, \mu_{Koeff(age)} = 0 \qquad H_A: \mu_{Koeff(age)} \neq 0\] Was hier also gemacht wird, ist ein t-Test für 1.16511 vs. \(\mu=0\). Unter P>|t| erkennen wir hier aber, dass die Irrtumswahrscheinlichkeit für die Ablehnung der \(H_0\) deutlich kleiner als 0,05 ist. Dementsprechend lehnen wir die Nullhypothese ab (wonach der Zusammenhang = 0 ist) und sprechen von einen statistisch signifikanten Zusammenhang.

9.5 Übungen 9

9.5.1 Übung 9-1

  1. Haben die Einkommensangaben von Mönnern eine höhere Varianz als die Einkommensangaben von Frauen?
  • Laden Sie den Allbus (Allbus_2018.dta) und wählen Sie alle Angaben für in Vollzeit arbeitende Befragte (work==1) aus, die ein Einkommen (inc) größer als 0 angebeben haben.
  • Denken Sie daran, die Missings mit . zu überschreiben!
  • Vergleichen Sie die Angaben des logarithmierten Einkommens der Befragten (gen log_inc = log(inc)) - durch die Logarithmierung werden die Einkommensangaben der NV angenähert. Die grundsätzliche Interpretation bleibt aber bestehen (höheres log_inc bedeutet auch höheres inc).
  • Wie lauten die Hypothesen für einen rechtsseitigen Test?
  • Vergleichen Sie die Varianz der (logarithmierten) Einkommensangaben in beiden Gruppen mit sdtest!
  • Wie lautet Ihre Entscheidung hinsichtlich der Hypothesen?

Zurück

9.5.2 Übung 9-2

  1. Waren im Jahr 2018 mehr als 4% der deutschen Bevölkerung Mitglied einer nicht-christlichen Glaubensgemeinschaft?
  • Laden Sie den Allbus (Allbus_2018.dta).
  • Wählen Sie alle Angaben aus, für welche die Konfession der Befragten vorliegt (rd01 > 0).
  • Erstellen Sie eine Dummyvariable, welche 1 ist wenn die Befragten einer nicht-christlichen Glaubensgemeinschaft angehören und 0 wenn sie einer christlichen oder keiner Glaubensgemeinschaft angehören (Hinweise)
  • Welcher Test ist hier der passende?
  • Formulieren Sie die Hypothesen
  • Führen Sie den Test durch
  • Wie lautet Ihre Entscheidung hinsichtlich der Hypothesen?

9.5.3 Übung 9-3

  1. Führen Sie eine ANOVA-Analyse des Vertrauens in staatliche Institutionen durch!
  • Nutzen Sie die unten aufgeführten Befehle, um einen gemeinsamen Indikator für Institutionenvertrauen zu erstellen!
  • Erklärung: Sehen Sie sich mit browse pt01 pt02 pt03 pt04 pt08 pt12 pt14 trust das Ergebnis an - trust ist jeweils der Mittelwert über die pt*-Variablen.
  • Können Sie Ost-West-Unterschiede beim Vertrauen in feststellen? Führen Sie eine ANOVA durch!
  • Nutzen Sie die eastwest als kategoriale Variable.
  • Führen Sie auch einen ttest und eine Regression durch - erkennen Sie die parallelen der Werte aus allen drei Modellen?
  • Nutzen Sie die Anleitung aus Kapitel 8.9, um die Differenzen zu visualisieren!
use "Allbus2018.dta", clear
mvdecode pt01 pt02 pt03 pt04 pt08 pt12 pt14, mv(-9) // missings raus
egen trust = rowmean(pt01 pt02 pt03 pt04 pt08 pt12 pt14) // Mittelwert über ptXX

9.6 ANOVA

ANOVA steht für analysis of variance und wird auch als univariate Varianzanalyse bezeichnet.

ANOVA wird verwendet, um Mittelwertunterschiede zwischen 2 oder mehr Gruppen zu vergleichen. Dies geschieht, indem die Varianz in den Daten betrachtet wird (daher der Name). Insbesondere vergleicht ANOVA das Ausmaß der Variation zwischen den Gruppen (between variance) mit dem Ausmaß der Variation innerhalb der Gruppen (within variance). Wir hatten diese Logik der Varianzzerlegung schon bei Regressionsmodellen kennengelernt:

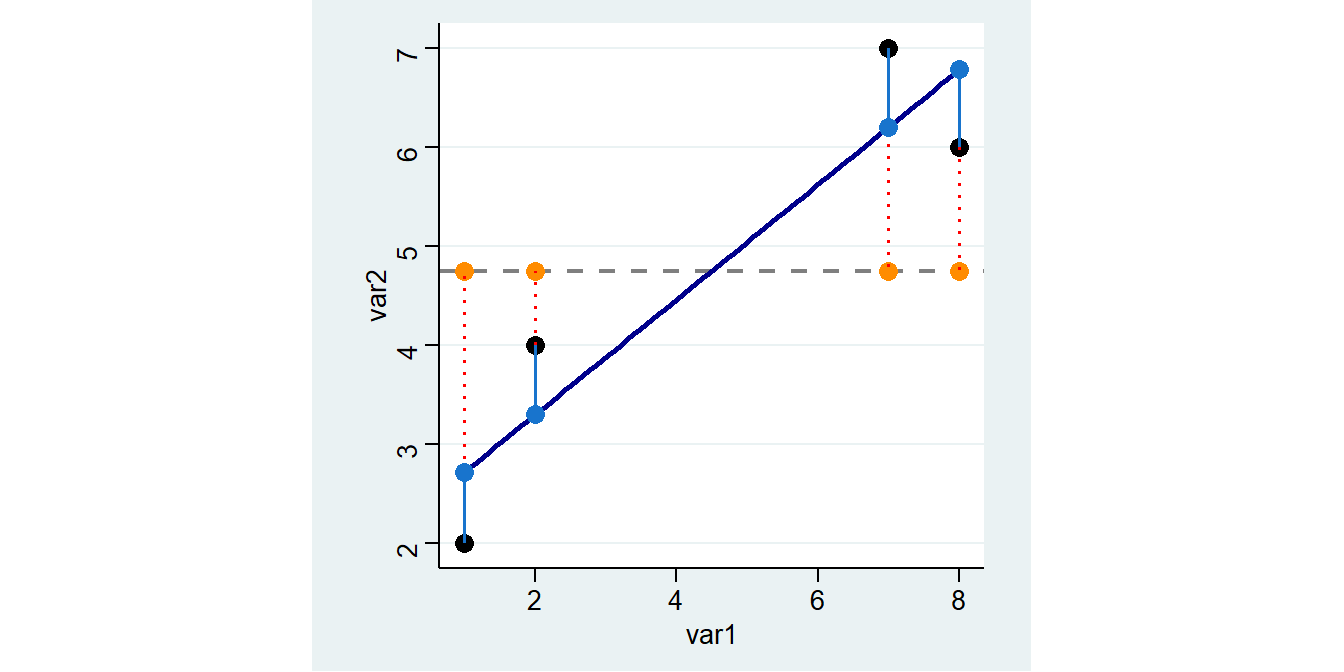
Hier hatten wir die Gesamtvarianz in erklärte und unerklärte Varianz zerlegt. Diese Sum of Squares bezeichnet Stata Model und Residual:

use "https://github.com/filius23/Stata_Skript/raw/master/regression_bsp.dta", clear
reg var2 var1
      Source |       SS       df       MS              Number of obs =       4
-------------+------------------------------           F(  1,     2) =   11.07
       Model |  12.4932432     1  12.4932432           Prob > F      =  0.0797
    Residual |  2.25675676     2  1.12837838           R-squared     =  0.8470
-------------+------------------------------           Adj R-squared =  0.7705
       Total |       14.75     3  4.91666667           Root MSE      =  1.0623

------------------------------------------------------------------------------
        var2 |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
        var1 |   .5810811   .1746331     3.33   0.080    -.1703044    1.332467
       _cons |   2.135135   .9485004     2.25   0.153    -1.945933    6.216203
------------------------------------------------------------------------------

Diese Logik überträgt ANOVA auf kategoriale Variablen, indem hier die Varianz in eine Streuung zwischen (between) und innerhalb der (within) der Gruppen aufgeteilt wird:

Aus diesen beiden Streuungen berechnen wir wieder Sum of squares, welche dann ins Verhältnis gesetzt werden, um den sog. F-Wertb zu berechnen:

\[F=\frac{\textbf{between}\;\texttt{Sum of Squares}}{\textbf{within}\;\texttt{Sum of Squares}}\]

Wenn der durchschnittliche Unterschied zwischen den Gruppen ähnlich ist wie innerhalb der Gruppen, beträgt das F-Verhältnis etwa 1. Wenn der durchschnittliche Unterschied zwischen den Gruppen größer wird als der innerhalb der Gruppen, wird das F-Verhältnis größer als 1. Um einen P-Wert zu erhalten, kann er gegen die F-Verteilung einer Zufallsvariablen mit den mit dem Zähler und Nenner des Verhältnisses verbundenen Freiheitsgraden getestet werden (ähnlich wie beim F-Test oben). Der P-Wert ist die Wahrscheinlichkeit, dieses oder ein größeres F-Verhältnis zu erhalten. Größere F-Verhältnisse ergeben kleinere P-Werte.

Mit oneway inc sex, tabulate bekommen wir bspw. die Varianzzerlegung der Einkommensangaben nach Geschlechtern:

cd ""
use Allbus2018.dta, clear
keep if inc > 0 & educ > 0
oneway inc sex, tabulate
            |             Summary of
            | BFR.:NETTOEINKOMMEN(OFFENE+LISTENAN
GESCHLECHT, |                GABE)
BEFRAGTE(R) |        Mean   Std. Dev.       Freq.
------------+------------------------------------
       MANN |   2214.3536   1519.8463        1612
       FRAU |   1403.8951   887.64216        1477
------------+------------------------------------
      Total |   1826.8343   1321.2263        3089

                        Analysis of Variance
    Source              SS         df      MS            F     Prob > F
------------------------------------------------------------------------
Between groups       506278204      1    506278204    319.98     0.0000
 Within groups      4.8843e+09   3087   1582201.17
------------------------------------------------------------------------
    Total           5.3905e+09   3088   1745638.99

Bartlett's test for equal variances:  chi2(1) = 419.3118  Prob>chi2 = 0.000

Die deskriptive Zusammenfassung oben liefert einige Deskriptionen: das arith. Mittel (Mean), die Standardabweichung (Std. Dev.) und die Stichprobengrößen (Freq.) für die abhängige Variable (Einkommen in unserem Beispiel) für jede Gruppe der unabhängigen Variable sex (also Frauen und Männer) sowie wenn alle Gruppen kombiniert werden (Total).

Die Stata-Ausgabe der einseitige ANOVA findet sich in der unteren Tabelle und zeigt an, ob wir einen statistisch signifikanten Unterschied zwischen unseren beiden Gruppenmittelwerten haben. Das Verhältnis von between und within wird unter F angegeben. Wir können sehen, dass das Signifikanzniveau Prob > F deutlich unter 0,05 liegt. Das legt einen statistisch signifikanten Unterschied im mittleren Einkommen den beiden Gruppen nahe.

Außerdem werden uns die Sum of Squares für die Unterschiede innerhalb und zwischen den Gruppen angezeigt. Wir sehen hier, dass die Varianz innerhalb der Gruppen die Gruppendifferenz deutlich übersteigt: die Sum of Squares zwischen den Gruppen sind mit 506278204 deutlich geringer als die Within-group SS 4.8843e+09. (4.8843e+09 steht für 4884300000, also 4.883 “mit dem Komma um 9 Stellen nach rechts verschoben”). Wir können aus den Zahlen für die Sum of Squares auch die Varianzaufklärung durch die Variable sex berechnen (between/Total):

dis  (506278204/ 5.3905e+09)
.09392045

Durch Kenntnis der Varibale sex können also 9.39% der gesamten Varianz (“Unterschiede”) des Einkommens erklärt werden.

9.6.1 ANOVA vs. t-Tests

Der t-Test wird beim Vergleich zweier Gruppen verwendet, während die ANOVA für den Vergleich von mehr als 2 Gruppen verwendet wird. Wenn wir den p-Wert unter Verwendung der ANOVA für 2 Gruppen berechnen, erhalten wir die gleichen Ergebnisse wie beim t-Test - hier also einen signifikanten Gruppenunterschied:

ttest inc, by( sex) unequ
Two-sample t test with equal variances
------------------------------------------------------------------------------
   Group |     Obs        Mean    Std. Err.   Std. Dev.   [95% Conf. Interval]
---------+--------------------------------------------------------------------
    MANN |    1612    2214.354    37.85447    1519.846    2140.104    2288.603
    FRAU |    1477    1403.895    23.09658    887.6422    1358.589    1449.201
---------+--------------------------------------------------------------------
combined |    3089    1826.834    23.77214    1321.226    1780.223    1873.445
---------+--------------------------------------------------------------------
    diff |            810.4585    45.30718                721.6233    899.2938
------------------------------------------------------------------------------
    diff = mean(MANN) - mean(FRAU)                                t =  17.8881
Ho: diff = 0                                     degrees of freedom =     3087

    Ha: diff < 0                 Ha: diff != 0                 Ha: diff > 0
 Pr(T < t) = 1.0000         Pr(|T| > |t|) = 0.0000          Pr(T > t) = 0.0000

9.6.2 ANOVA vs. lineare Regression

Die lineare Regression wird zur Analyse kontinuierlicher Beziehungen verwendet; die Regression ist jedoch im Wesentlichen die gleiche wie die ANOVA. Bei der ANOVA berechnen wir Mittelwerte und Abweichungen unserer Daten von den Mittelwerten. Bei der linearen Regression berechnen wir die beste Linie durch die Daten und berechnen die Abweichungen der Daten von dieser Linie. Stata gibt uns das F-Verhältnis bei Regressionsmodellen direkt mit aus. Zu beachten ist aber hier, dass wir für eine kategoriale unabhängige Variable i. voranstellen müssen:

reg inc i.sex
(388 observations deleted)

      Source |       SS       df       MS              Number of obs =    3089
-------------+------------------------------           F(  1,  3087) =  319.98
       Model |   506278204     1   506278204           Prob > F      =  0.0000
    Residual |  4.8843e+09  3087  1582201.17           R-squared     =  0.0939
-------------+------------------------------           Adj R-squared =  0.0936
       Total |  5.3905e+09  3088  1745638.99           Root MSE      =  1257.9

------------------------------------------------------------------------------
         inc |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
         sex |
       FRAU  |  -810.4585   45.30718   -17.89   0.000    -899.2938   -721.6233
       _cons |   2214.354   31.32913    70.68   0.000     2152.926    2275.782
------------------------------------------------------------------------------
  • die obere Tabelle entspricht dem Output von oneway:
    • die Sum of Squares innerhalb von sex betragen 506278204, zwischen sex ist die Sum of Squares (4.8843e+09)
    • Das Verhältnis der within und between Streuung beträgt F(1, 3087) = 319.98 (siehe Spalte F in oneway)
    • die Variable sex kann 9,38% der Streuung der Einkommen erklären (R-squared = 0.0938), siehe unsere Berechnung oben
  • die untere Tabelle entspricht dem ttest:
    • Frauen verdienen im Mittel 806.5515 weniger als Männer und dieser Unterschied ist statistisch signifikant (vgl. diff bei ttest)

Übungen 3

9.7 ANOVA mehrere Gruppen

Der Vorteil von ANOVA ist aber, dass sich auch Gruppenunterschiede für Variablen mit mehr als zwei Ausprägungen untersuchen lassen, bspw. Schulbildungsniveaus:

oneway inc educ, tabulate
            |             Summary of
ALLGEMEINER | BFR.:NETTOEINKOMMEN(OFFENE+LISTENAN
SCHULABSCHL |                GABE)
        USS |        Mean   Std. Dev.       Freq.
------------+------------------------------------
  OHNE ABSC |   1066.0244   836.64603          41
  VOLKS-,HA |   1413.4075   946.82151         724
  MITTLERE  |   1610.9124   912.21029        1073
  FACHHOCHS |   2165.1172   1373.9449         273
  HOCHSCHUL |   2336.9612   1714.1057         954
  ANDERER A |   1415.3125   964.18503          16
  NOCH SCHU |     548.125   544.93733           8
------------+------------------------------------
      Total |   1826.8343   1321.2263        3089

                        Analysis of Variance
    Source              SS         df      MS            F     Prob > F
------------------------------------------------------------------------
Between groups       492795287      6   82132547.9     51.68     0.0000
 Within groups      4.8977e+09   3082   1589142.74
------------------------------------------------------------------------
    Total           5.3905e+09   3088   1745638.99

Bartlett's test for equal variances:  chi2(6) = 520.5203  Prob>chi2 = 0.000

Wir erkennen:

  • dass signifikante Gruppenunterschiede bestehen: Prob > F ist deutlich < 0,05
  • Kenntnis von educ kann
  • dass Befragte mit Hochschulreife die höchsten Durchschnittseinkommen haben (Mean = 2336.9612), Schüler*innen die niedrigsten (Mean = 548.125) usw.

Auch hier der Vergleich zu Regressionsmodellen einer kategorialen UV:

reg inc i.educ
      Source |       SS       df       MS              Number of obs =    3089
-------------+------------------------------           F(  6,  3082) =   51.68
       Model |   492795287     6  82132547.9           Prob > F      =  0.0000
    Residual |  4.8977e+09  3082  1589142.74           R-squared     =  0.0914
-------------+------------------------------           Adj R-squared =  0.0896
       Total |  5.3905e+09  3088  1745638.99           Root MSE      =  1260.6

-------------------------------------------------------------------------------------
                inc |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
--------------------+----------------------------------------------------------------
               educ |
VOLKS-,HAUPTSCHULE  |   347.3831   202.3723     1.72   0.086    -49.41508    744.1812
    MITTLERE REIFE  |    544.888   200.6006     2.72   0.007     151.5636    938.2125
FACHHOCHSCHULREIFE  |   1099.093   211.1412     5.21   0.000     685.1011    1513.085
    HOCHSCHULREIFE  |   1270.937   201.0606     6.32   0.000     876.7106    1665.163
 ANDERER ABSCHLUSS  |   349.2881   371.5925     0.94   0.347     -379.306    1077.882
     NOCH SCHUELER  |  -517.8994   487.2396    -1.06   0.288    -1473.247    437.4478
                    |
              _cons |   1066.024   196.8745     5.41   0.000     680.0058    1452.043
-------------------------------------------------------------------------------------

\(\rightarrow\) hier sind die Koeffizienten jeweils auf den Vergleich zu educ=1 zu interpretieren:

  • Befragte mit VOLKS-,HAUPTSCHULE verdienen im Schnitt 347.3831 EUR mehr als Befragte ohne Abschluss (educ = 1). Der Unterschied ist aber nicht statistisch signifikant (P>|t| > 0,05).
  • Befragte mit MITTLERE REIFE verdienen im Schnitt 544.888 EUR mehr als Befragte ohne Abschluss (educ = 1). Der Unterschied ist statistisch signifikant (P>|t| < 0,05).
  • Befragte mit FACHHOCHSCHULREIFE verdienen im Schnitt 1099.093 EUR mehr als Befragte ohne Abschluss (educ = 1). Der Unterschied ist statistisch signifikant (P>|t| < 0,05).
  • Befragte, die noch zur Schule gehen, verdienen im Schnitt 517.8994 EUR weniger als Befragte ohne Abschluss (educ = 1). Der Unterschied ist statistisch signifikant (P>|t| < 0,05).

Wir können die Referenzgruppe mit ib3. auf Realschulabsolvent*innen setzen:

reg inc ib3.educ
      Source |       SS       df       MS              Number of obs =    3089
-------------+------------------------------           F(  6,  3082) =   51.68
       Model |   492795287     6  82132547.9           Prob > F      =  0.0000
    Residual |  4.8977e+09  3082  1589142.74           R-squared     =  0.0914
-------------+------------------------------           Adj R-squared =  0.0896
       Total |  5.3905e+09  3088  1745638.99           Root MSE      =  1260.6

-------------------------------------------------------------------------------------
                inc |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
--------------------+----------------------------------------------------------------
               educ |
    OHNE ABSCHLUSS  |   -544.888   200.6006    -2.72   0.007    -938.2125   -151.5636
VOLKS-,HAUPTSCHULE  |  -197.5049   60.62983    -3.26   0.001    -316.3839   -78.62597
FACHHOCHSCHULREIFE  |   554.2048   85.45211     6.49   0.000      386.656    721.7537
    HOCHSCHULREIFE  |   726.0488   56.09631    12.94   0.000     616.0589    836.0388
 ANDERER ABSCHLUSS  |  -195.5999    317.494    -0.62   0.538    -818.1212    426.9214
     NOCH SCHUELER  |  -1062.787   447.3521    -2.38   0.018    -1939.926    -185.649
                    |
              _cons |   1610.912   38.48412    41.86   0.000     1535.455     1686.37
-------------------------------------------------------------------------------------

\(\rightarrow\) jetzt sind die Koeffizienten jeweils auf den Vergleich zu educ=3 zu interpretieren:

  • Befragte mit VOLKS-,HAUPTSCHULE verdienen im Schnitt 197.5049 EUR weniger als Befragte Realschulabschluss (educ = 3). Der Unterschied ist statistisch signifikant (P>|t| < 0,05).
  • Befragte mit FACHHOCHSCHULREIFE verdienen im Schnitt 554.2048 EUR mehr als Befragte Realschulabschluss (educ = 3). Der Unterschied ist statistisch signifikant (P>|t| < 0,05).
  • Befragte mit HOCHSCHULREIFE verdienen im Schnitt 726.0488 EUR mehr als Befragte Realschulabschluss (educ = 3). Der Unterschied ist statistisch signifikant (P>|t| < 0,05).
  • Befragte mit anderem Abschluss verdienen im Schnitt 195.5999 EUR weniger als Befragte Realschulabschluss (educ = 3). Der Unterschied ist aber nicht statistisch signifikant (P>|t| > 0,05).
  • Befragte, die noch zur Schule gehen, verdienen im Schnitt 1062.78 EUR weniger als Befragte Realschulabschluss (educ = 3). Der Unterschied ist statistisch signifikant (P>|t| < 0,05).

  1. Andernfalls hätten wir sex umdrehen müssen, zB so: gen sex_reverse = 3-sex. So bekommen dann Frauen die 1 und Männer die 2 zugewiesen und Stata setzt bei sdtest hs16, by(sex_reverse) dann die Varianz der Frauen in den Zähler.↩︎